Помогите пожалуйста 4 и 5 номера

Ответы
Ответ:
4. Расстояние от точки В до прямой равно 8 см.
5. Периметр трапеции равен 62 см.
Объяснение:
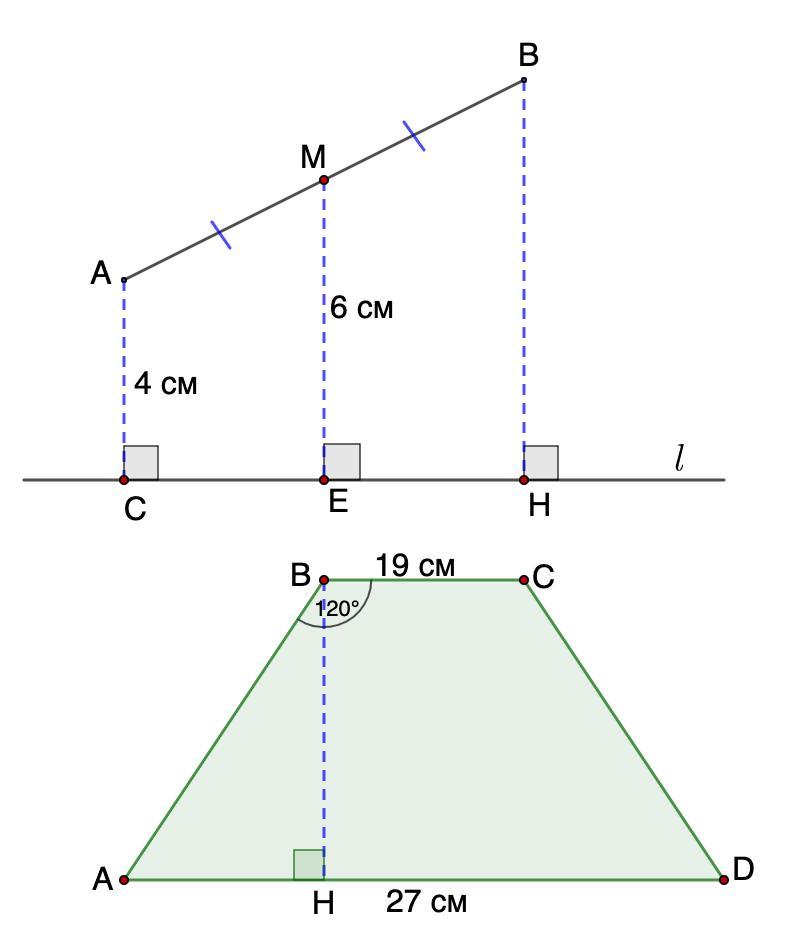
4. Точки А и В лежат по одну сторону от прямой , точка М - середина отрезка АВ. Расстояния от точек А и М до прямой
соответственно равны 4 см и 6 см. Найдите расстояние от точки В до прямой
.
5. В равнобедренной трапеции ABCD основания AD = 27 см, ВС = 19 см, В=120°. Найдите периметр трапеции.
4. Дано: прямая ;
АМ = МВ;
АС = 4 см; МЕ = 6 см.
Найти: ВН.
Решение:
- Расстояние от точки до прямой - длина перпендикуляра, опущенного из данной точки на прямую.
⇒ АС ⊥ ; МЕ ⊥
; ВН ⊥
.
- Если две прямые перпендикулярны третьей, то они параллельны между собой.
⇒ AC || ME || BH.
САВН - прямоугольная трапеция.
АМ = МВ;
- Если на одной из двух прямых отложить последовательно несколько равных между собой отрезков и через их концы провести параллельные прямые, пересекающие вторую прямую, то они отсекут на второй прямой равные между собой отрезки.
⇒ СЕ = ЕН.
Тогда МЕ - средняя линия трапеции САВН.
- Средняя линия равна полусумме оснований.
Расстояние от точки В до прямой равно 8 см.
5. Дано: ABCD - равнобедренная трапеция;
AD = 27 см, ВС = 19 см, В=120°.
Найти: Р(ABCD)
Решение:
Периметр - сумма длин всех сторон трапеции.
Два основания известны.
Надо найти боковую сторону.
- Углы, прилежащие к боковой стороне трапеции в сумме равны 180°.
⇒ ∠А = 180° - ∠В = 180° - 120° = 60°
Рассмотрим ΔАВН - прямоугольный (ВН - высота)
- Высота, проведенная из вершины тупого угла равнобедренной трапеции делит большее основание на части, меньшая из которых равна полуразности оснований.
⇒ АН = (AD - BC) : 2 = (27 - 19) : 2 = 4 (см)
- Сумма острых углов прямоугольного треугольника равна 90°.
⇒ ∠АВН = 90° - ∠А = 90° - 60° = 30°
- Катет, лежащий против угла в 30°, равен половине гипотенузы.
⇒ АВ = АН · 2 = 4 · 2 = 8 (см)
АВ = CD = 8 см.
Р(ABCD) = AB + BC + CD + AD = 8 + 19 + 8 + 27 = 62 (см)
Периметр трапеции равен 62 см.