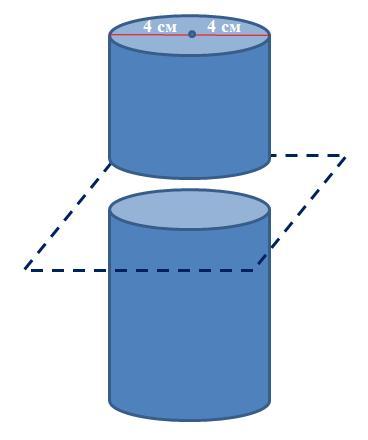
Циліндр, радіус основи якого дорівнює 4 см, висота — 12 см, перетнули площиною, паралельною до його основи. Утворилося два циліндри. Визначте суму площ повних поверхонь утворених циліндрів
Ответы
Ответ:
Сумма площадей полных поверхностей образовавшихся цилиндров равна 160·π см²
Пошаговое объяснение:
Перевод: Цилиндр, радиус основания которого равен 4 см, высота - 12 см, пересекли плоскостью, параллельной его основанию. Образовалось два цилиндра. Определите сумму площадей полных поверхностей образовавшихся цилиндров.
Нужно знать. Формула для нахождения полной поверхности цилиндра через высоту H и радиус основания R:
S(цилиндр) = 2·π·R·H+2·π·R².
Решение. По условию R = 4 см и H = 12 см. Тогда полная поверхность цилиндра (см. рисунок 1):
S(цилиндр) = 2·π·4·12+2·π·4² = 96·π+32·π = 128·π см².
После деления плоскостью, параллельной его основанию (см. рисунок 2) образуется 2 цилиндра, сумма полной поверхности которых отличается двумя основаниями от исходного цилиндра.
Поэтому сумма площадей S полных поверхностей образовавшихся цилиндров равна:
S = S(цилиндр) + 2·π·R² = 128·π + 2·π·4² = 128·π + 32·π = 160·π см².
#SPJ1