Предмет: Математика,
автор: steampro5b
Диагонали прямоугольника MNKL пересекаются в точке O . Найди площадь треугольника OKL , если MK=24 , а ∠KOL=30° .
Ответы
Автор ответа:
0
∆ОКL - треугольник образованный из двух полудиагоналей, OK И OL, и одной стороны KL прямоугольника.
Формула площади треугольника:
S = ab sin(7), где а, b стороны треугольника и Ө - угол между этими сторонами.
Нам дана длина диагонали (у прямоугольника длины диагоналей равны) МК=24.
Диагонали прямоугольника пересекаются в центре, тогда OK=OL=24/2=12.
Угол <KOL - это и есть угол между диагоналями.
Пошаговое объяснение:
Площадь треугольника ∆ОKL=36
Приложения:
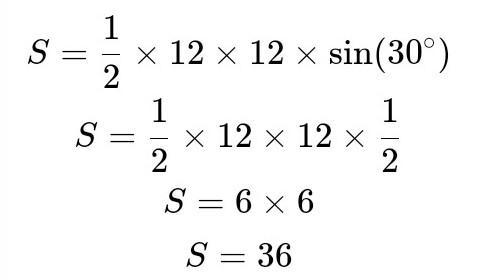
Похожие вопросы
Предмет: Қазақ тiлi,
автор: ulan9459
Предмет: Английский язык,
автор: vertildenis77
Предмет: Английский язык,
автор: malikova9621
Предмет: Физкультура и спорт,
автор: LamaMa1