Предмет: Алгебра,
автор: Аноним
Помогите решить Алгебру. Даю 30 баллов
Приложения:
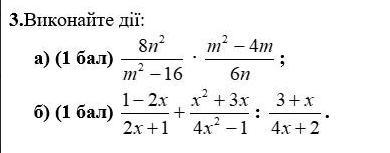
Ответы
Автор ответа:
1
Ответ:
a)
б)
Объяснение:
а) по формуле:
б) по формулам: ;
Похожие вопросы
Предмет: Математика,
автор: prizmagod
Предмет: Другие предметы,
автор: tamerlanzakirov188
Предмет: Қазақ тiлi,
автор: Аноним
Предмет: География,
автор: Аноним
Предмет: Українська мова,
автор: chulevich2019r