Предмет: Геометрия,
автор: lirita249
прошу, помогите, сегодня уже нужно сдать
Приложения:
ГАЗ52:
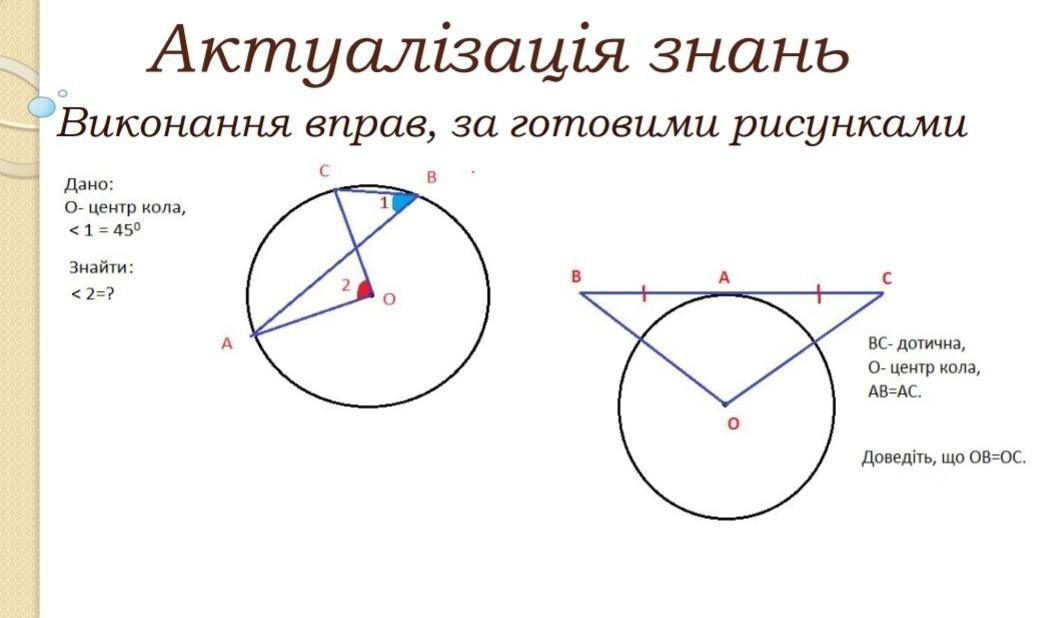
1) <2=<1=45, тк это вписанные углы, опирающиеся на одну дугу.
2) А точка касания. Тогда радиус ОА перпендикулярен касательной ВС. ЗНАЧИТ ПРЯМОУГОЛЬНЫЕ треугольники АОВ и АОС равны по 2 каретам. Тогда остальные элементы равны. Поэтому ОВ= ОС.
угол 2 НЕ вписанный!
Спасибо. Ошибка.
а мне то что делать, я уже записала
1) <2=2•<1=90, тк это вписанный угол равен половине дуги, а центральный дуге на которую опирается.
да благословит вас бог)
natalyabryukhova вам пишет ответ.
Ответы
Автор ответа:
1
Ответ:
1. Угол 2 равен 90°.
2. Доказано, что ОВ = ОС.
Объяснение:
Решить задачи по готовым рисункам.
1. Дано: окр.О;
∠1 = 45°;
Найти: ∠2.
Решение:
- Вписанный угол равен половине градусной меры дуги, на которую он опирается.
∠1 - вписанный.
⇒ ◡АС = 2∠1 = 45° · 2 = 90°
- Центральный угол равен градусной мере дуги, на которую он опирается.
∠2 - центральный.
⇒ ∠2 = ◡АС = 90°
Угол 2 равен 90°.
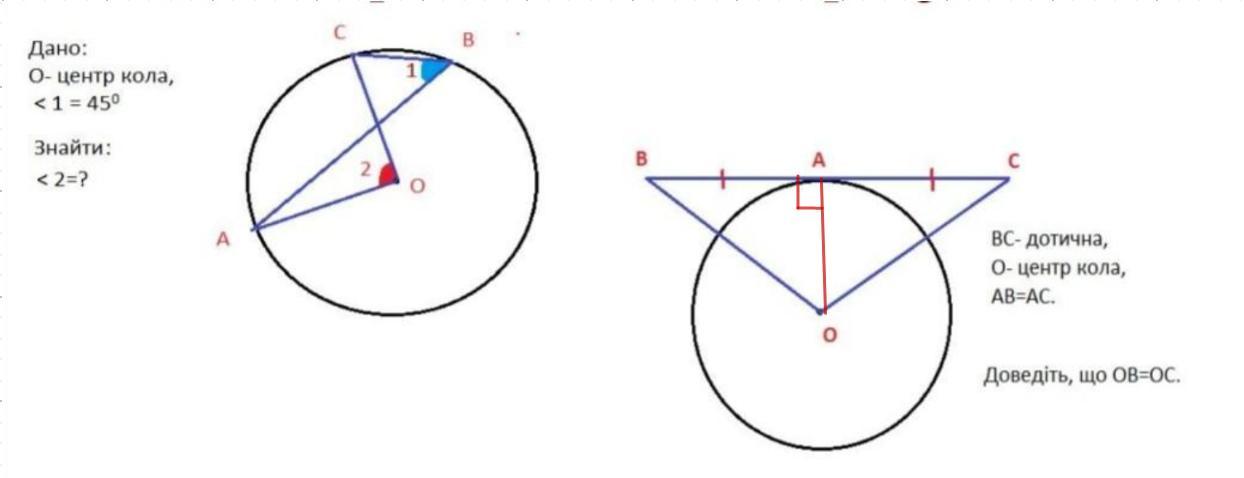
2. Дано: Окр.О;
ВС - касательная;
АВ = АС.
Доказать: ОВ = ОС.
Доказательство:
Рассмотрим ΔОВС.
- Радиус, проведенный в точку касания, перпендикулярен касательной.
⇒ ОА - высота.
АВ = АС (условие)
⇒ ОА - медиана.
- Если в треугольнике высота является медианой, то этот треугольник - равнобедренный.
⇒ ОВ = ОС.
Доказано, что ОВ = ОС.
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: p77973288
Предмет: Литература,
автор: Ogurechik2012
Предмет: Окружающий мир,
автор: asemhamidullina
Предмет: Математика,
автор: zorjanalen
Предмет: Математика,
автор: ALGEBRICHKA