Предмет: Алгебра,
автор: vivivivivigug
Помогите, пожалуйста.Нужно упростить, объясняя свои действия . На уровне 10 класса.
Приложения:
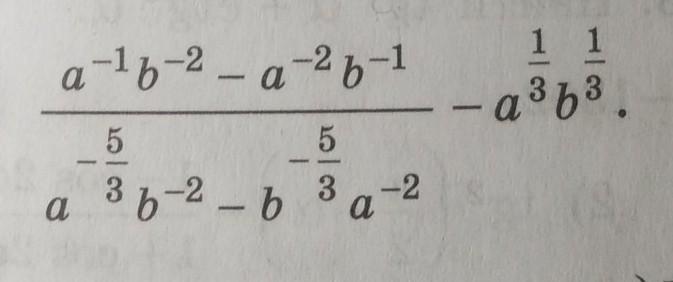
Ответы
Автор ответа:
2
Решение.
Упростить выражение . Применяем формулу сокращённого умножения: разность кубов . А также действия со степенями с дробными показателями .
vivivivivigug:
Спасибо!
Пожалуйста .
Похожие вопросы
Предмет: Русский язык,
автор: matrizaevavera
Предмет: Математика,
автор: d49815048
Предмет: Химия,
автор: rabalay952
Предмет: История,
автор: sasaaremkiv
Предмет: Русский язык,
автор: adderlykristen