Question

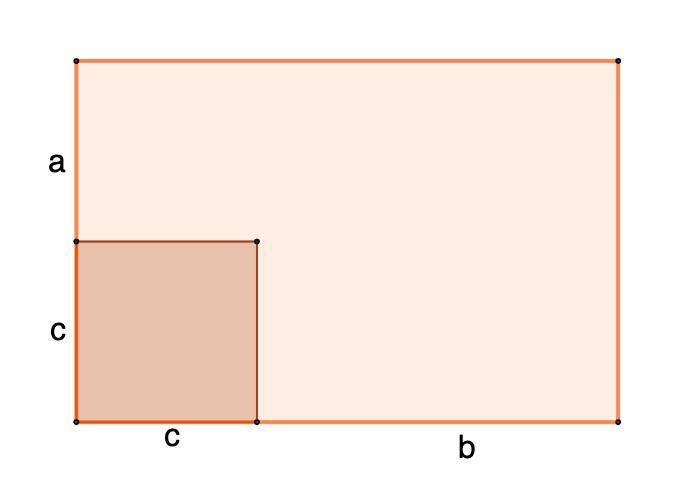
Одна сторона прямокутника більша за сторону квадрата на а см, а інша сторона цього самого прямокутника більша від сторони того самого квадрата на b см. Запиши формулу обчислення сторони квадрата, якщо його площа менша від площі прямокутника на S см², та знайди сторону квадрата, якщо а = 3, b = 5, S = 47.​

Answer 1

Ответ:

$\displaystyle\bf c=\frac{S-ab}{a+b}$ - формула вычисления стороны квадрата.

Сторона квадрата равна 4 см.

Объяснение:

Одна сторона прямоугольника больше стороны квадрата на а см, а другая сторона этого прямоугольника больше стороны того же квадрата на b см. Запиши формулу вычисления стороны квадрата, если его площадь меньше площади прямоугольника на S см² и найди сторону квадрата, если а = 3, b = 5, S = 47.​

Пусть сторона квадрата с см.

Тогда ширина прямоугольника (с + а) см, длина прямоугольника - (с + b) см.

• Площадь квадрата равна квадрату его стороны.

Sкв. = с²

• Площадь прямоугольника равна произведению смежных сторон.

Sпр. = (c + a)(c + b) = c² + bc + ac + ab.

Sпр. - Sкв. = S

c² + bc + ac + ab - c² = S

bc + ac + ab = S

c(b + a) = S - ab

Выразим сторону квадрата с:

$\displaystyle\bf c=\frac{S-ab}{a+b}$ - формула вычисления стороны квадрата.

Найдем сторону квадрата, если а = 3 см, b = 5 см, S = 47 см².

$\displaystyle\bf c=\frac{S-ab}{a+b}=\frac{47-3\cdot5}{3+5}= \frac{32}{8}=4$  (cм)

Сторона квадрата равна 4 см.

#SPJ1