Question

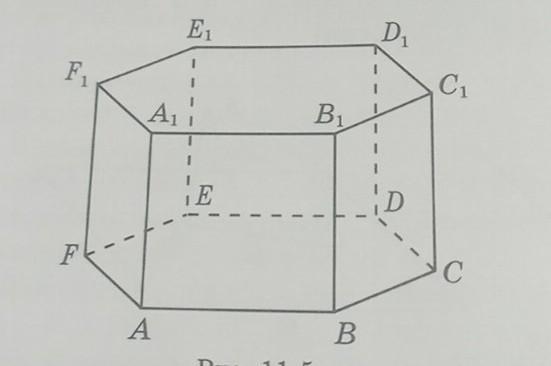
Для правильной шестиугольной призмы доказать перпендикулярность прямых : 1)АВ и ВD1 , 2)АВ и ЕА1 , 3)АС и DC1.
​

Answer 1

Объяснение:

ПРАВИЛЬНОМ 6-УГОЛЬНИКЕ ВСЕ СТОРОНЫ РАВНЫ И КАЖДЫЙ УГОЛ РАВЕН 120°.

РАССТОЯНИЕМ ОТ ТОЧКИ ДО ПЛОСКОСТИ ЯВЛЯЕТСЯ ПЕРПЕНДИКУЛЯР, ПРОВЕДЁННЫЙ ОТ ДАННОЙ ТОЧКИ К ДАННОЙ ПЛОСКОСТИ

Расстоянием от точки до плоскости является перпендикуляр.

а) меньшая диагональ правильного 6-угольника перпендикулярна его стороне, поэтому АВ⏊ВД

б) диагональ ВЕ является диаметром описанной окружности вокруг 6-угольника и является биссектрисой угла В и делит его пополам, поэтому ∠АВН =120÷2=60°. Проведём перпендикуляр АН к ВЕ, и получим прямоугольный треугольник АВН с прямым углом АНВ, катетами АН и ВН и гипотенузой АВ. Найдём АН, используя синус угла:

AH=AB×sinABH=1×sin60°=1×√3/2=√3/2

РЕШЕНИЕ ПУНКТА а) НА ФОТО!