Question

Висота правильної чотирикутної зрізаної піраміди дорівнює 12 см. Сторони основ 20 см і 38 см. Знайти:
1) довжину її бічного ребра;
2) площу перерізу, який проходить через діагоналі основ;
3) площу поверхні.

Answer 1

Ответ:

1) довжина ребра 3√34 см

2) площа перерізу 348√2 см²

3) площа поверхні 3584 см²

Объяснение:

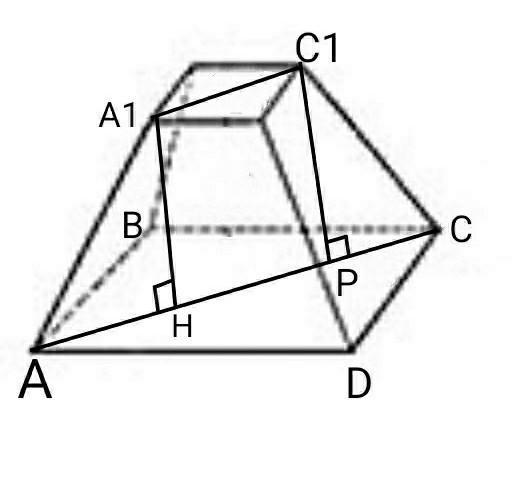
А1С1=А1В1√2=20√2 см

АС=АВ√2=38√2 см

А1С1=НР=20√2 см

АН=РС

РС=(АС-НР)/2=(38√2-20√2)/2=9√2 см

∆С1РС- прямокутний трикутник

За теоремою Піфагора:

С1С=√(С1Р²+РС²)=√(12²+(9√2)²)=

=√(144+162)=√306=3√34 см

_____________

2)

S(AA1C1C)=C1P(A1C1+AC)/2=12(20√2+38√2)/2=

=12*58√2/2=348√2 см²

______________

3)

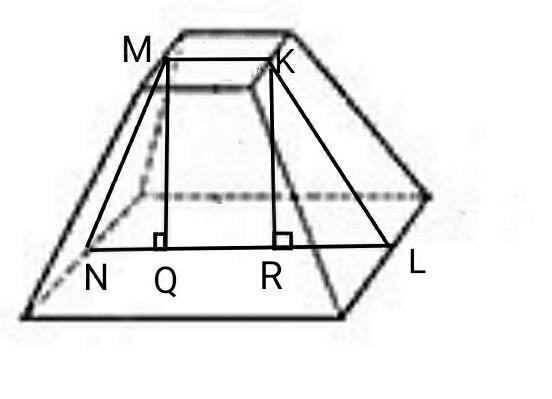
MK=A1B1=20см

NL=AB=38см

RL=(NL-MK)/2=(38-20)/2=9см

∆КRL- прямокутний трикутник

За теоремою Піфагора:

КL=√(KR²+RL²)=√(12²+9²)=

=√(144+81)=√225=15 см

Sбіч=½(4*АВ+4*А1В1)*КL=

=½(4*20+4*38)*15=½(80+152)*15=

=½*232*15=1740см²

Sосн1=АВ²=38²=1444см²

Sосн2=А1В1²=20²=400см²

Sпов=Sбіч+Sосн1+Sосн2=1740+1444+400=

=3584 см²