Предмет: Алгебра,
автор: hsjwiwj
ПОЖАЛУЙСТА ОЧЕНЬ СРОЧНО
решите уравнение
Приложения:
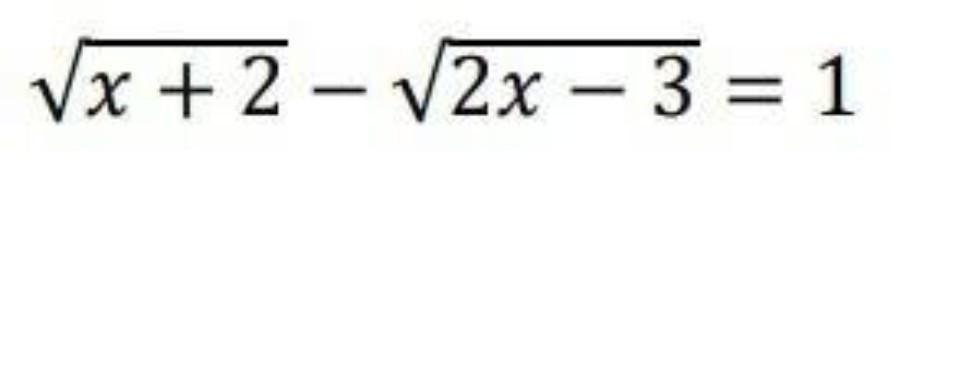
Ответы
Автор ответа:
1
Ответ:
Ответ: 2.
Объяснение:
Решить уравнение:
- Подкоренное выражение неотрицательно.
ОДЗ:
x ∈ [1,5; +∞)
Уединим корень. Перенесем второй корень вправо, поменяв знак на противоположный:
Возведем обе части в квадрат:
Еще раз уединим корень и возведем обе части в квадрат:
Обязательно выполним проверку:
х = 14
⇒ 14 не является корнем данного уравнения.
х = 2
Верно.
Ответ: 2.
Похожие вопросы
Предмет: Математика,
автор: sasanikolaenko176
Предмет: Українська мова,
автор: lerabozok196
Предмет: Литература,
автор: maranmaslanik
Предмет: Математика,
автор: sidirlubov
Предмет: Химия,
автор: petrovychvolodimir8