Question

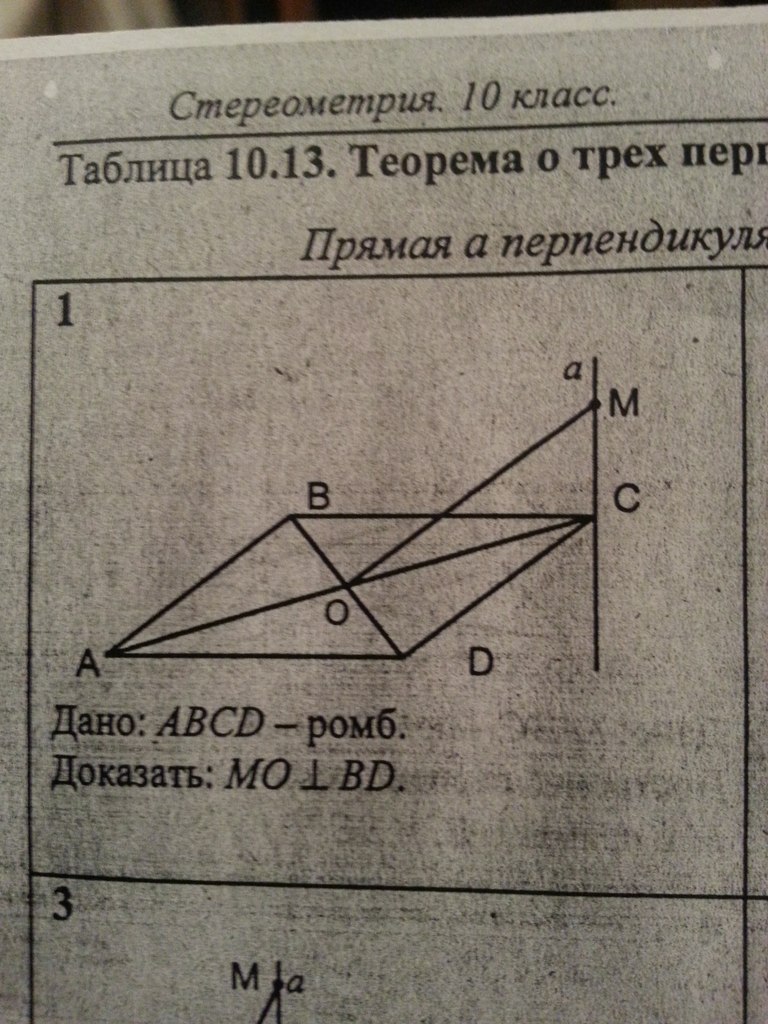
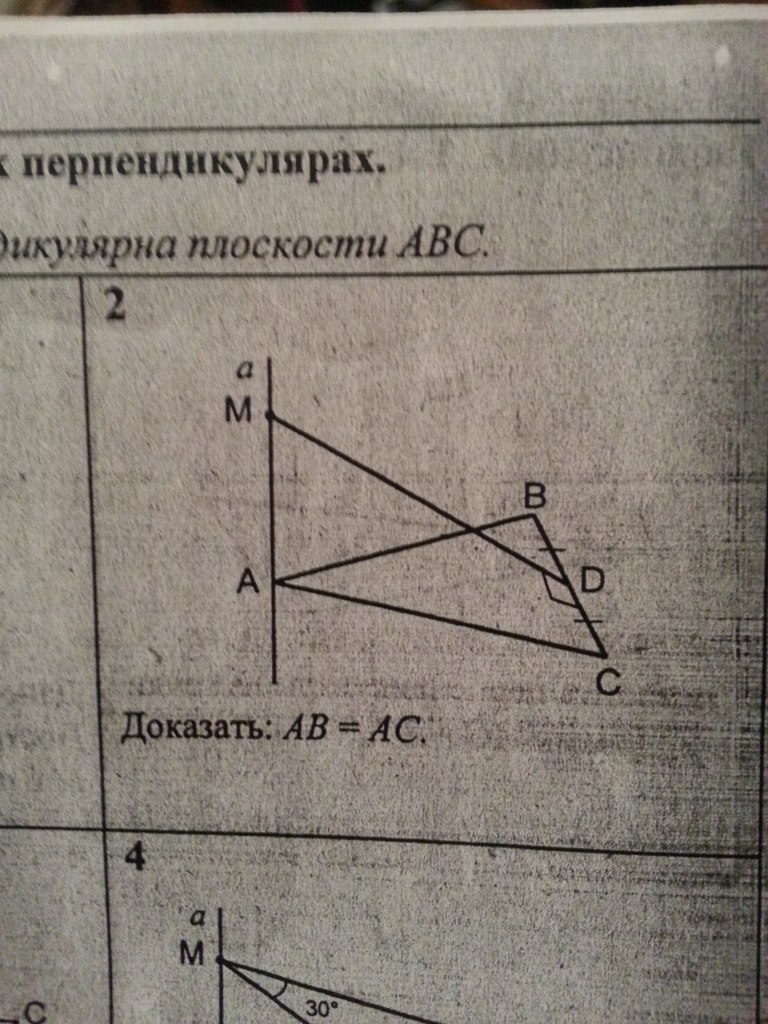
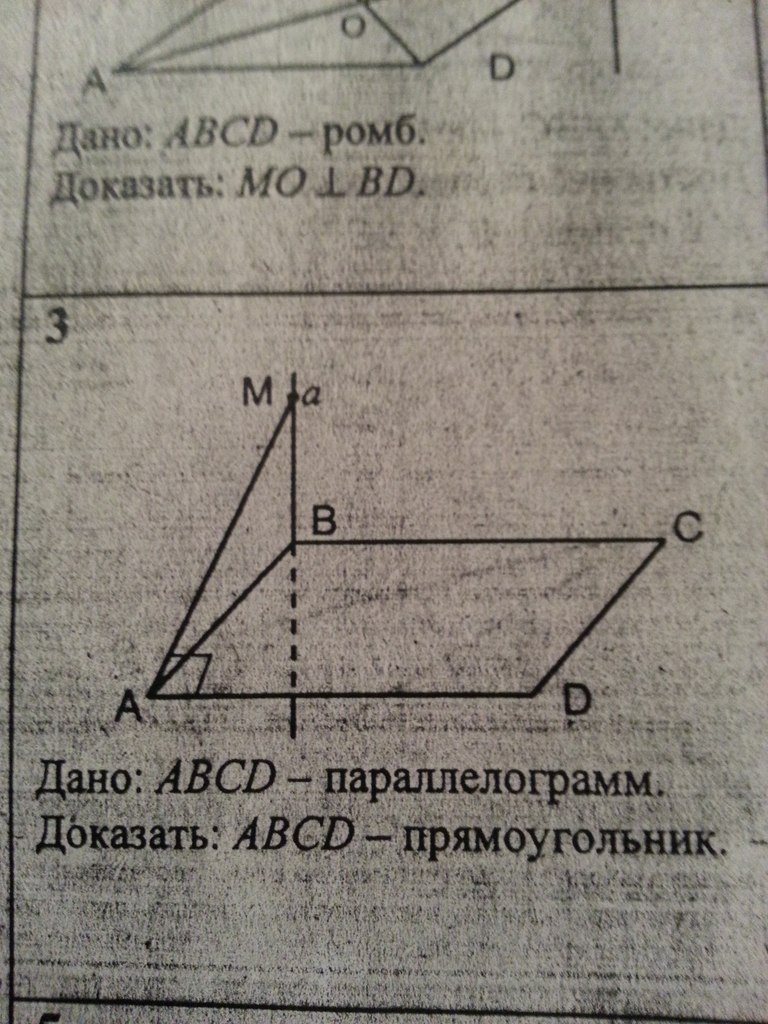
Добрый вечер. Вопросы касательно геометрии, а конкретно темы: Теорема о трех перпендикулярах. Относительно каждой задачи: Прямая a перпендикулярна плоскости ABC. Тут нужны доказательства. Заранее спасибо!

Answer 1

прямая МС перпендикулярна плоскости АВС, треугольник МОС прямоугольный, АВСД -ромб, диагонали ромба пресекаются под углом 90, ВО перпендикулярна СО, теорема - если прямая (ВО), которая проведена на плоскости (АВСД) перпендикулярна к проекции (СО - проекция МО) наклонной (МО -наклонная) то прямая (ВО) перпендикулярна и к самой наклонной (МО), МО перпендикулярна ВО, значит МО перпендикулярна ВД  №2 МА перпендикулярна плоскости АВС , МД перпендикулярна ВС, проводим проекцию МД на ВС = АД, теорема о трех перпендикулярах (обратная), - прямая (ВС), которая проведена на плоскости перпендикулярна к наклонной (МД), то она (ВС) перпендикулярна и к проекции (АД) этой наклонной (МД), АД перпендикулярна ВС, ВД=СД, АД=медиана=высота, только в равнобедренном треугольнике высота проведенная из вершины угла =медиане, треугольник АВС равнобедренный, АВ=АС, №3 МВ перпендикулярна АВС, АМВ-прямоугольный треугольник , АВ проекция АМ на плоскость, МА перпендикулярна АД, согласно теореме о трех перпендикулярах (обратная, см.выше) АВ перпендикулярна АД, АВСД-параллелограмм , уголВАД=90, теорема-если в параллелограмме есть прямой угол то параллелограмм - прямоугольник, АВСД-прямоугольник