Предмет: Математика,
автор: fotyniaohlu
Знайдіть суму. Срочно, даю максимум баллов. Прошу нету времени.
Приложения:
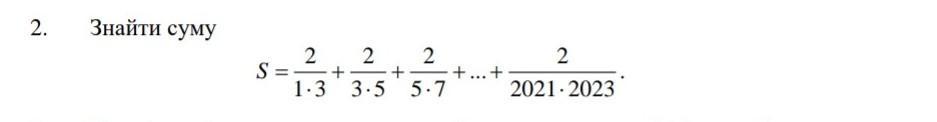
Ответы
Автор ответа:
3
Ответ:
Пошаговое объяснение:
Заметим что
Таким образом мы можем вынести 1/2 , и все сократится кроме
первого и последнего числа
Похожие вопросы
Предмет: Английский язык,
автор: anastasiayaroslavcev
Предмет: Химия,
автор: KiraIaskevevych
Предмет: Українська мова,
автор: Аноним
Предмет: Математика,
автор: naida0005