Предмет: Алгебра,
автор: ndjfjbc
помогите решить пожалуйста
с объяснением расписать
Приложения:
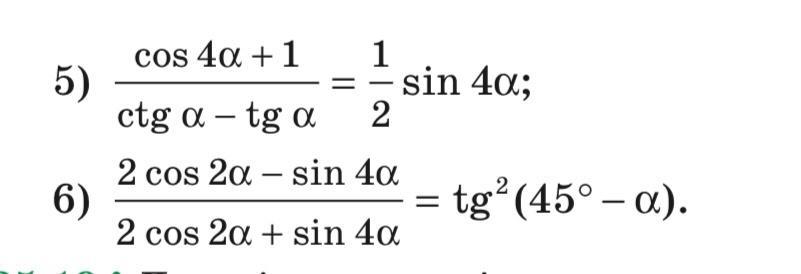
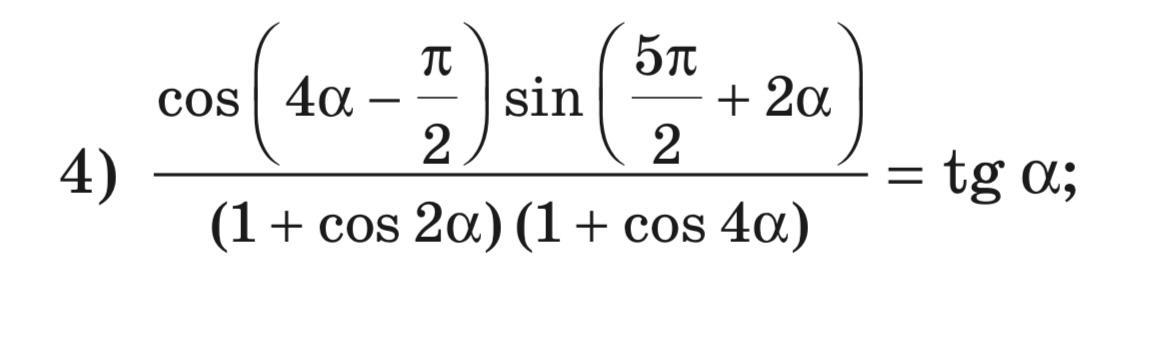
Ответы
Автор ответа:
2
Ответ:
Применяем формулы двойных углов и формулу тангенса разности
А также потребуются формулы приведения в 3 примере .
spamgg002:
помогите у профиле пожалуйста
Похожие вопросы
Предмет: История,
автор: recoverixz
Предмет: Русский язык,
автор: ramiba2022b
Предмет: Литература,
автор: eppvlinova
Предмет: Українська література,
автор: rqwesda
Предмет: Информатика,
автор: amina616