Предмет: Алгебра,
автор: gavrik148290
докажите, что значение выражения не зависит от значения переменной
Приложения:
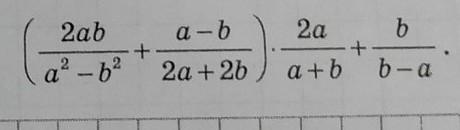
Ответы
Автор ответа:
0
Ответ:
1
Объяснение:
((2ab)/(a²-b²) +(a-b)/(2a+2b))·(2a)/(a+b) +b/(b-a)=1
1) (2ab)/(a²-b²) +(a-b)/(2a+2b)=(2ab)/((a-b)(a+b) +(a-b)/(2(a+b))=(4ab+(a-b)²)/(2(a-b)(a+b))=(4ab+a²-2ab+b²)/(2(a-b)(a+b))=(a²+2ab+b²)/(2(a-b)(a+b))=(a+b)²/(2(a-b)(a+b))=(a+b)/(2(a-b))
2) (a+b)/(2(a-b)) ·(2a)/(a+b)=a/(a-b)
3) a/(a-b) +b/(b-a)=a/(a-b) -b/(a-b)=(a-b)/(a-b)=1
Вывод: значение данного выражения не зависит от значения переменной.
Похожие вопросы
Предмет: Биология,
автор: arina241464
Предмет: Французский язык,
автор: kerolinaa
Предмет: Қазақ тiлi,
автор: aruzhanshagatai
Предмет: Математика,
автор: Аноним
Предмет: География,
автор: bogvsego