Предмет: Алгебра,
автор: snifockek
ребят. срочно. 20 баллов! с решением и объяснением, пожалуйста
Приложения:

Ответы
Автор ответа:
0
Ответ:на фото
Объяснение:
Приложения:
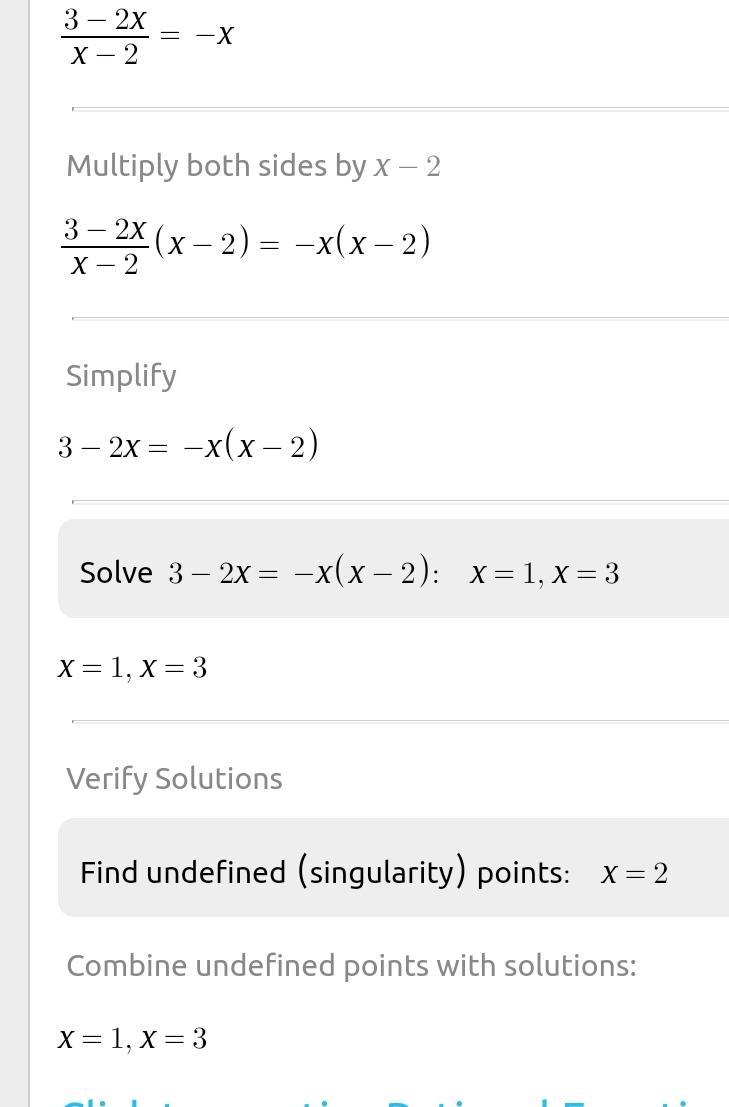

Автор ответа:
1
Ответ:
a)
найдём область допустимых значений:
сокращаем на общий делитель x-2:
б)
Похожие вопросы
Предмет: Українська мова,
автор: nikimaschenko123
Предмет: Українська мова,
автор: windiwalker59
Предмет: Математика,
автор: maksimkarcacenka3
Предмет: Математика,
автор: Аноним
Предмет: История,
автор: dimarudenk