Предмет: Алгебра,
автор: annakazimirova27
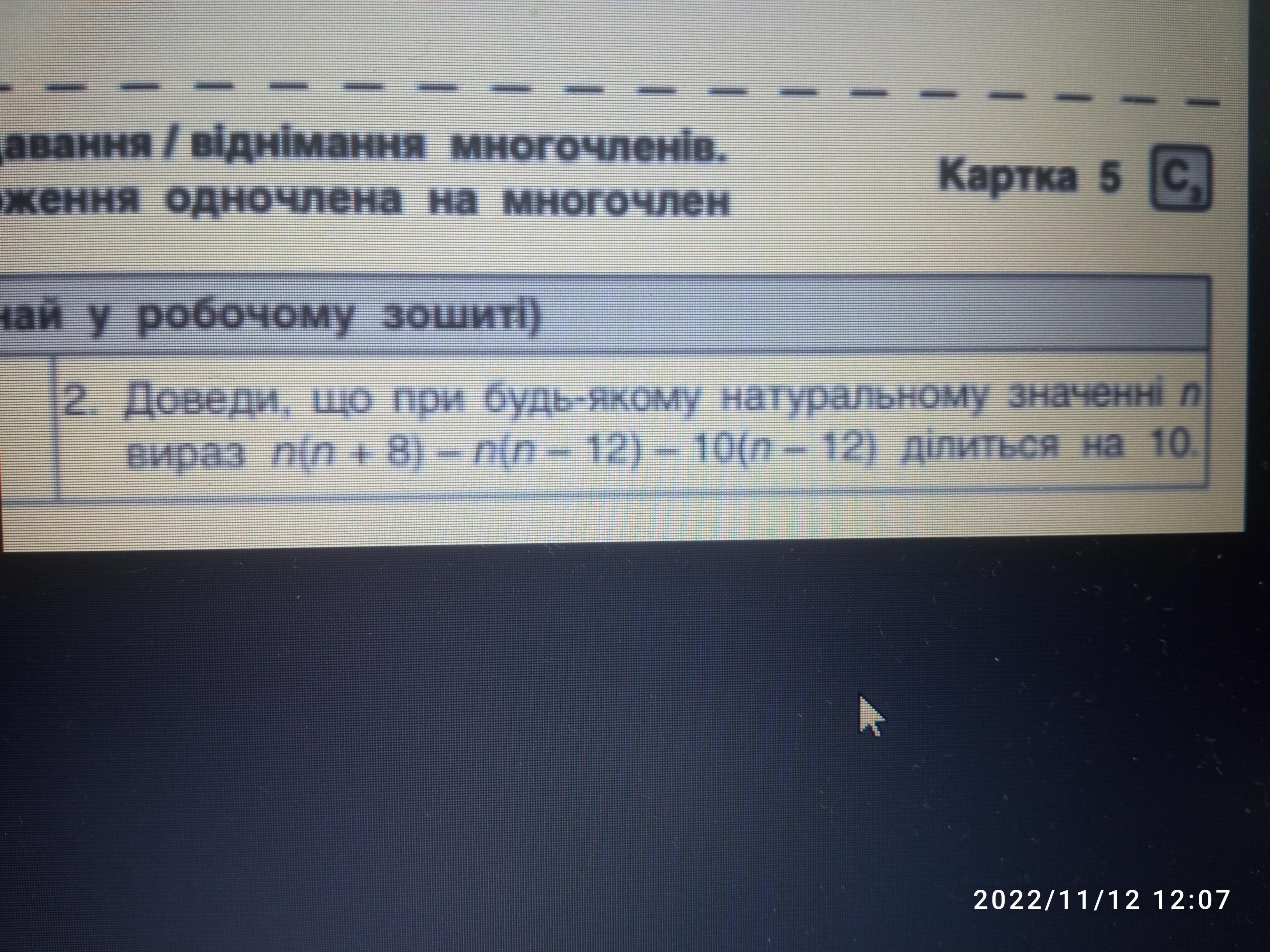
Доведіть що при будь-якому натуральному значенні n ділиться на 10
Приложения:
Ответы
Автор ответа:
2
Ответ:
Объяснение:
n ( n+8) - n ( n -12) - 10 ( n -12) =
= n^2 +8 n - n^2+12 n -10 n +120 n =
= 10 n +120 n = 130 n.
в числе 130 последняя цифра 0, значит при любом n в конце будет также ноль ( например n = 8, 130 *8 = 1040). А все, что оканчивается на ноль всегда делится на 10.
sergeevaolga5:
Неверно раскрыта последняя скобка.
где?
Автор ответа:
2
Доказательство:
В результате преобразования алгебраического выражения получили произведение числа 10 и суммы чисел (n+12). Полученное произведение, при любом значении переменной n будет делится на 10, т.к. один из его множителей равен 10. Следовательно, на 10 делится и исходное алгебраическое выражение.
Что и требовалось доказать.
Дякую тобі велике
Похожие вопросы
Предмет: Физика,
автор: DinerII
Предмет: Физика,
автор: yaroslavaredej
Предмет: Литература,
автор: participantbrain
Предмет: Химия,
автор: i68948575
Предмет: Биология,
автор: kirishimaMelody