Предмет: Алгебра,
автор: ADHpepo
Допоможіть розібратись
Ділення многочленів у стовпчик
Алгебра
Приложения:
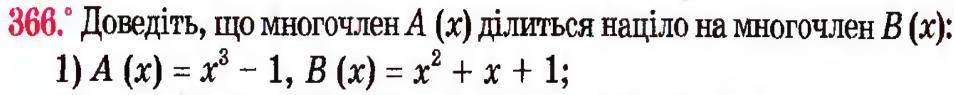
Ответы
Автор ответа:
1
Дивіться прикріплене фото
Приложения:
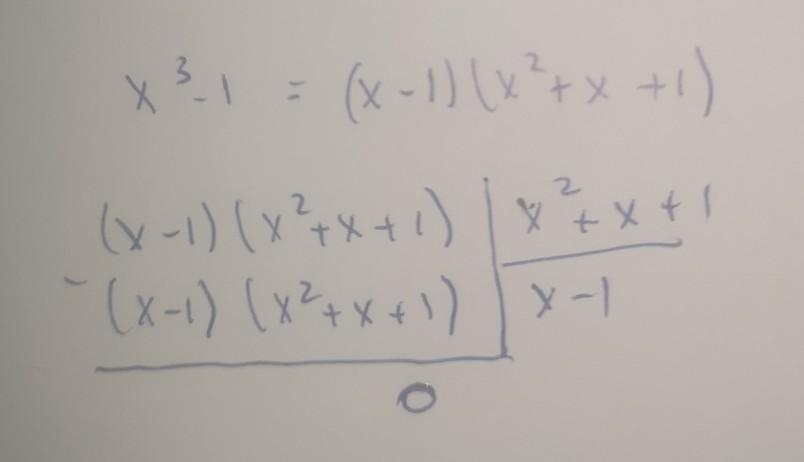
Автор ответа:
2
Ответ:
Так как многочлен А(х) можно разложить на множители
, то при делении А(х) на В(х)=х²+х+1
произойдёт сокращение одинаковых множителей .
Деление уголком фактически не потребуется .
Но можно и разделить .
Похожие вопросы
Предмет: Қазақ тiлi,
автор: dm66778899221
Предмет: Українська мова,
автор: Lyubomir228
Предмет: Английский язык,
автор: aleksrodrigo70
Предмет: Английский язык,
автор: 2009music
Предмет: Биология,
автор: prosttdisadisa