Предмет: Алгебра,
автор: Аноним
Решить методом Гаусса
Приложения:
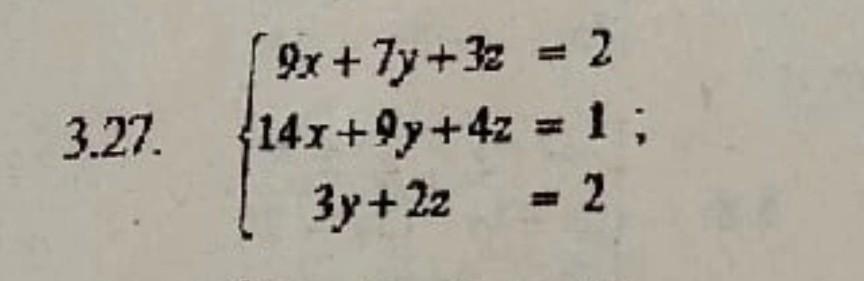
Ответы
Автор ответа:
1
Ответ:
Решить систему методом Гаусса .
Запишем расширенную матрицу системы .
Обратный ход.
Ответ: .
Приложения:

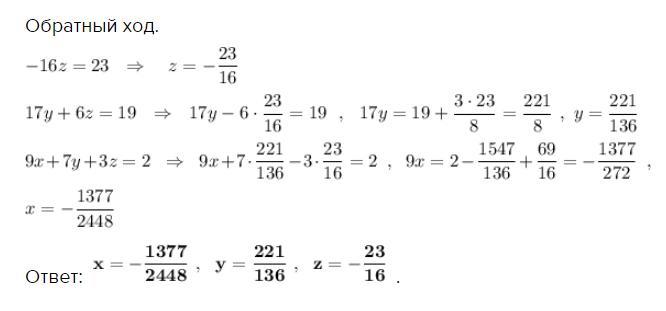
NNNLLL54:
добавила
Похожие вопросы
Предмет: Химия,
автор: abibasppp2
Предмет: Алгебра,
автор: Mimish12
Предмет: Математика,
автор: artemp0504
Предмет: Математика,
автор: asetkartoeva06606
Предмет: История,
автор: 3dima52