Предмет: Геометрия,
автор: nyurossi
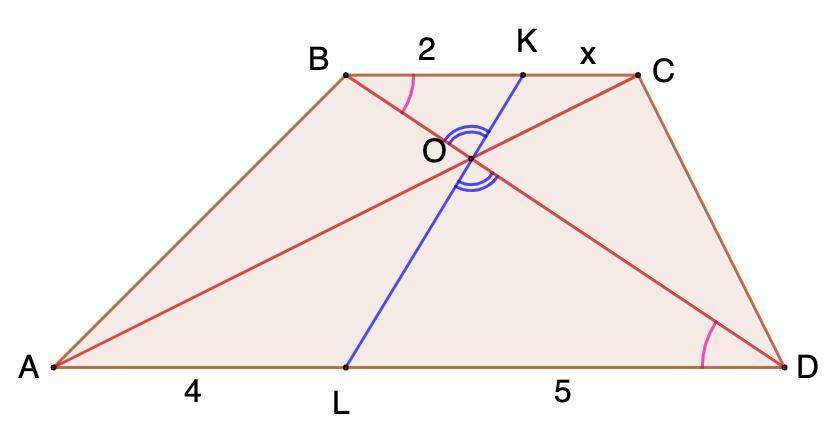
На основаниях BC и AD трапеции abcd отмечены точки K и L соответственно. Отрезок KL проходит через точку пересечения диагоналей. Найдите трезок KC, если AL=4, LD=5, BK=2
Ответы
Автор ответа:
5
Ответ:
Отрезок KL равен (ед).
Объяснение:
На основаниях BC и AD трапеции ABCD отмечены точки K и L соответственно. Отрезок KL проходит через точку пересечения диагоналей. Найдите трезок KC, если AL=4, LD=5, BK=2.
Дано: ABCD - трапеция;
К ∈ ВС; L ∈AD.
AL = 4, LD = 5, BK = 2.
АС ∩ BD = Oβ
Найти: КС
Решение:
1. Рассмотрим ΔОВК и ΔLOB.
- При пересечении двух параллельных прямых третьей накрест лежащие углы равны.
⇒ ∠ОВК = ∠ODL (накрест лежащие при BC || AD и секущей BD.
- Вертикальные углы равны.
⇒ ВОК = ∠LOD (вертикальные).
ΔОВК ~ ΔLOB (по двум углам)
Напишем отношения сходственных сторон:
2. Рассмотрим ΔОКС и ΔAOL.
∠KCO = ∠OAL (накрест лежащие при ВС || AD и секущей АС)
∠KOC = ∠AOL (вертикальные)
⇒ ΔОКС ~ ΔAOL (по двум углам)
Напишем отношения сходственных сторон:
Отрезок KL равен (ед).
#SPJ1
Приложения:
nyurossi:
спасибо
Похожие вопросы
Предмет: История,
автор: kodirovarejhan
Предмет: Алгебра,
автор: lizagrib315
Предмет: Математика,
автор: uhajnackij
Предмет: Алгебра,
автор: Аноним