Предмет: Алгебра,
автор: louezor21228
ПОМОЖІТЬ БУДЬ ОАСОЧКАААААА
Приложения:
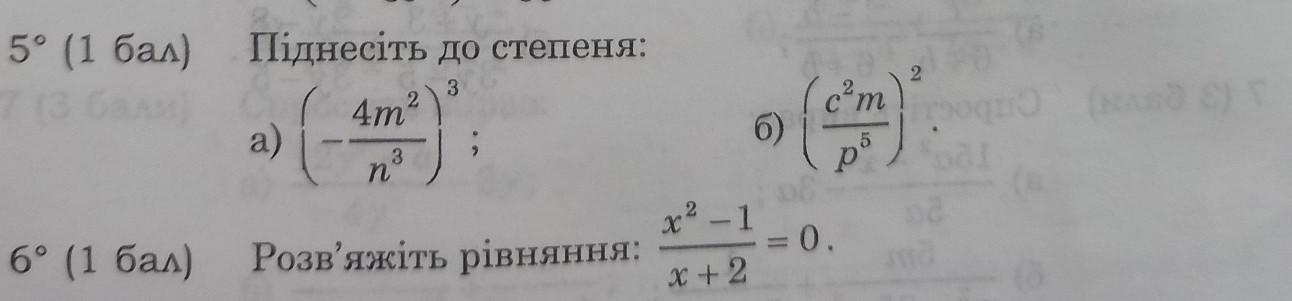
Ответы
Автор ответа:
0
Ответ:
5) Применяем свойства:
Дробь равна 0, если числитель равен 0, а знаменатель не равен 0 .
Ответ:
Автор ответа:
0
Ответ:
5.
а)
б)
6.
( x - 1 )( x + 1 ) = 0
( x - 1 ) = 0; ( x + 1 ) = 0
= 1;
= -1
Похожие вопросы
Предмет: Алгебра,
автор: andreika93xaxa
Предмет: Қазақ тiлi,
автор: asel201818
Предмет: Қазақ тiлi,
автор: rajyssaken80
Предмет: Алгебра,
автор: ChikibamBoniD
Предмет: Математика,
автор: Hika1209