Предмет: Геометрия,
автор: Аноним
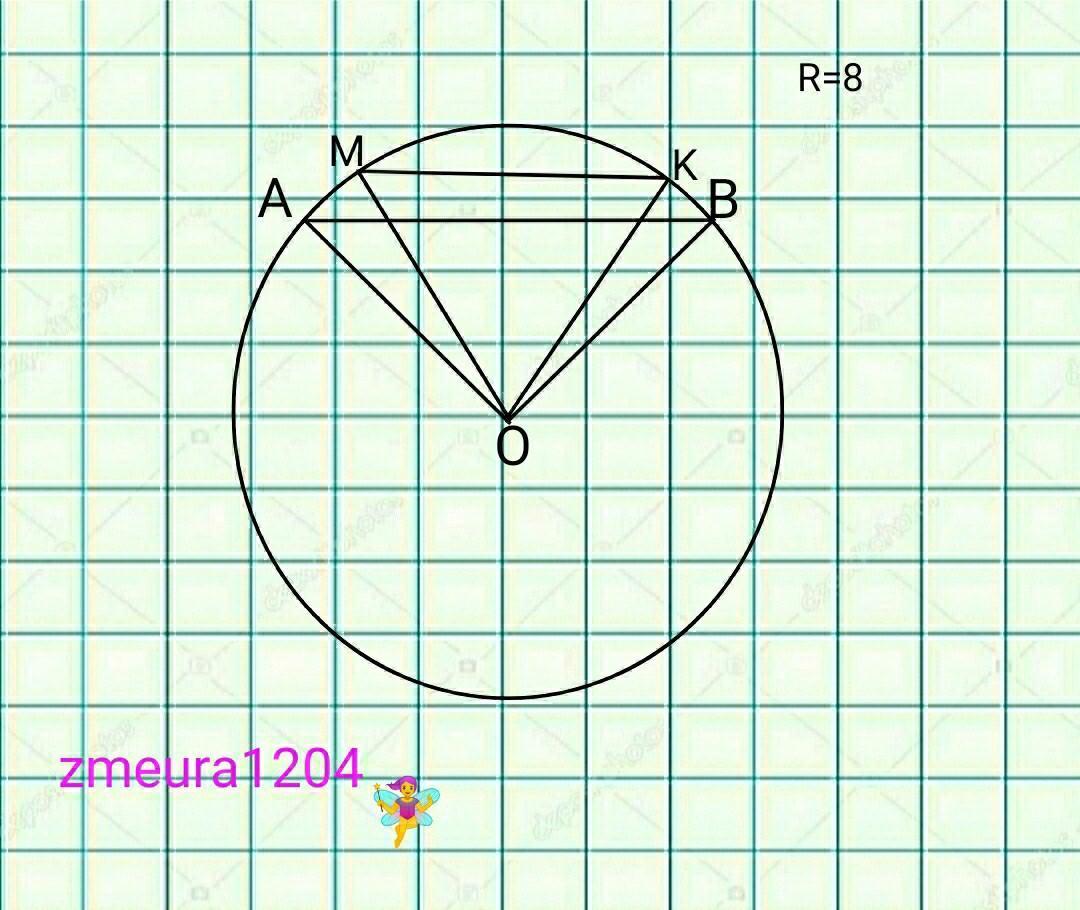
Радіус круга дорівнює 8 см. По один бік від його центра проведено дві паралельні хорди, які дорівнюють відповідно сторонам квадрата і правильного шестикутника, вписаних в цей круг. Знайти частину круга, яка знаходиться між хордами.
Ответы
Автор ответа:
1
Відповідь:
(16π-96+48√3)/3
Объяснение:
АВ- хорда, що дорівнює стороні квадрата
∠АОВ=90° (діагоналі квадрата перетинаються під прямим кутом)
МК- хорда, що дорівнює стороні шестикутника
∠МОК=60° правильний шестикутник поділяється на 6 рівносторонніх трикутників.)
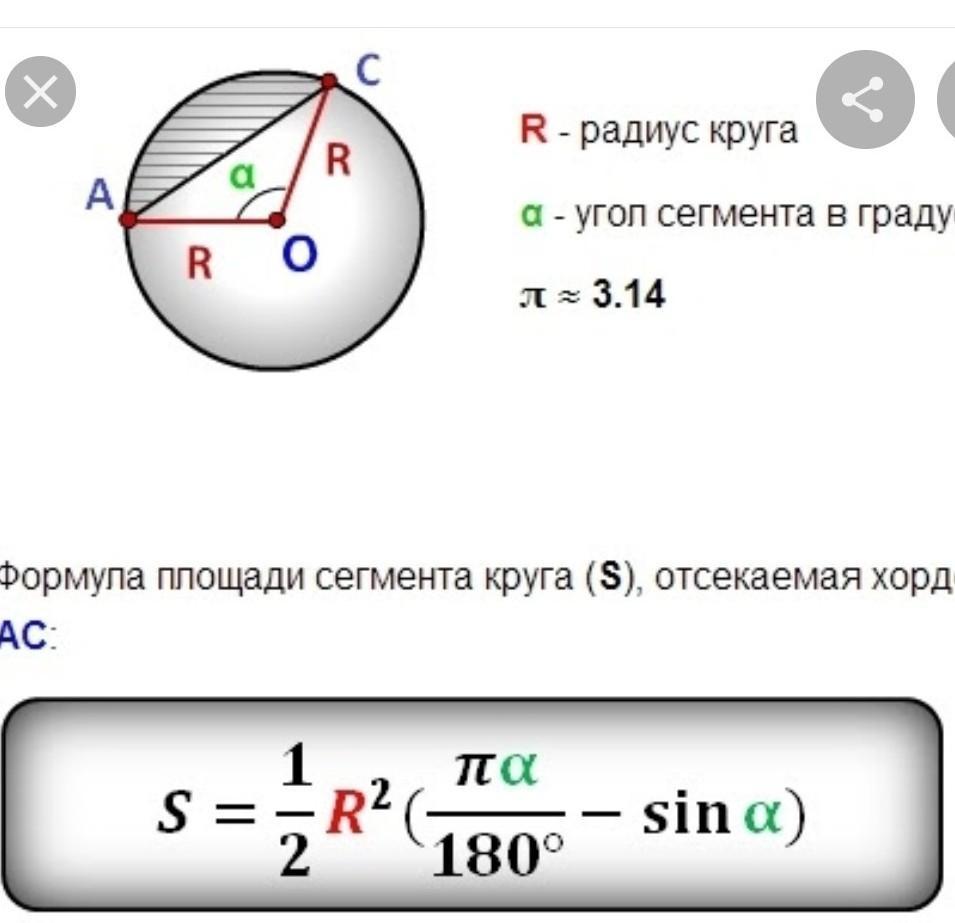
Sсегм1=½*R²(π*90°/180°-sin90°)=
=½*8²(π/2-1)=32(π/2-1)=16π-32 см²
Sсегм2=½*R²(π*60°/180°-sin60°)=
=½*64(π/3-√3/2)=32π/3-16√3=
32π/3-16*3√3/3=(32π-48√3)/3.
S(АМКВ)=Sсегм1-Sсегм2=
=16π-32-(32π-48√3)/3=
=16π*3/3-32*3/3-(32π-48√3)/3=
=(48π-96-32π+48√3)/3=
=(16π-96-48√3)/3
Приложения:
zmeura1204:
В формуле заштрихованн сегмент.
Треугольники вообще не берите во внимание.
https://prnt.sc/p78OSaynmUqy
https://prnt.sc/EEocr4PDAX-K
https://prnt.sc/dDhe5gEalTSC
Похожие вопросы
Предмет: География,
автор: alinarozko47
Предмет: Химия,
автор: sasaletenko79
Предмет: История,
автор: taisiadance
Предмет: Русский язык,
автор: marucia2575