Предмет: Математика,
автор: 20Lenok20
1. Случайным образом выбирают одно из решений неравенства –1 ≤ 2x + 3 ≤ 9. Какова вероятность того, что оно удовлетворяет неравенству x ≥ 0? 2. Середины сторон прямоугольника являются вершинами ромба. Какова вероятность того, что наугад выбранная точка прямоугольника окажется внутри ромба, если стороны прямоугольника равны 6 см и 8 см?
Ответы
Автор ответа:
0
Решим для начала неравенства:

Длина промежутка равна 3 - (-2) = 3+2 = 5
Общее решение с x≥0 есть промежуток [0;3] длина которого - (3-0=3)
Искомая вероятность, по определению геометрической вероятности

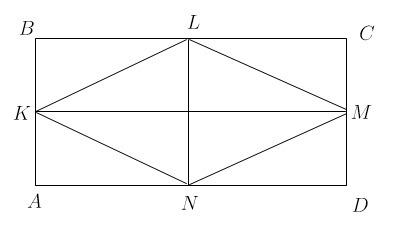
Задача 2. Из рисунка видим, что и
и 
Площадь ромба KLMN:
Площадь прямоугольника ABCD:
По определению геометрической вероятности:
Длина промежутка равна 3 - (-2) = 3+2 = 5
Общее решение с x≥0 есть промежуток [0;3] длина которого - (3-0=3)
Искомая вероятность, по определению геометрической вероятности
Задача 2. Из рисунка видим, что
Площадь ромба KLMN:
Площадь прямоугольника ABCD:
По определению геометрической вероятности:
Приложения:
Похожие вопросы
Предмет: Математика,
автор: surgut161017
Предмет: Физика,
автор: meetonspy89
Предмет: Физика,
автор: balakinaarina2018
Предмет: Биология,
автор: wandersx