Предмет: Алгебра,
автор: kerbel3310
Розв'язати рівняння за формулою Бінома
Приложения:
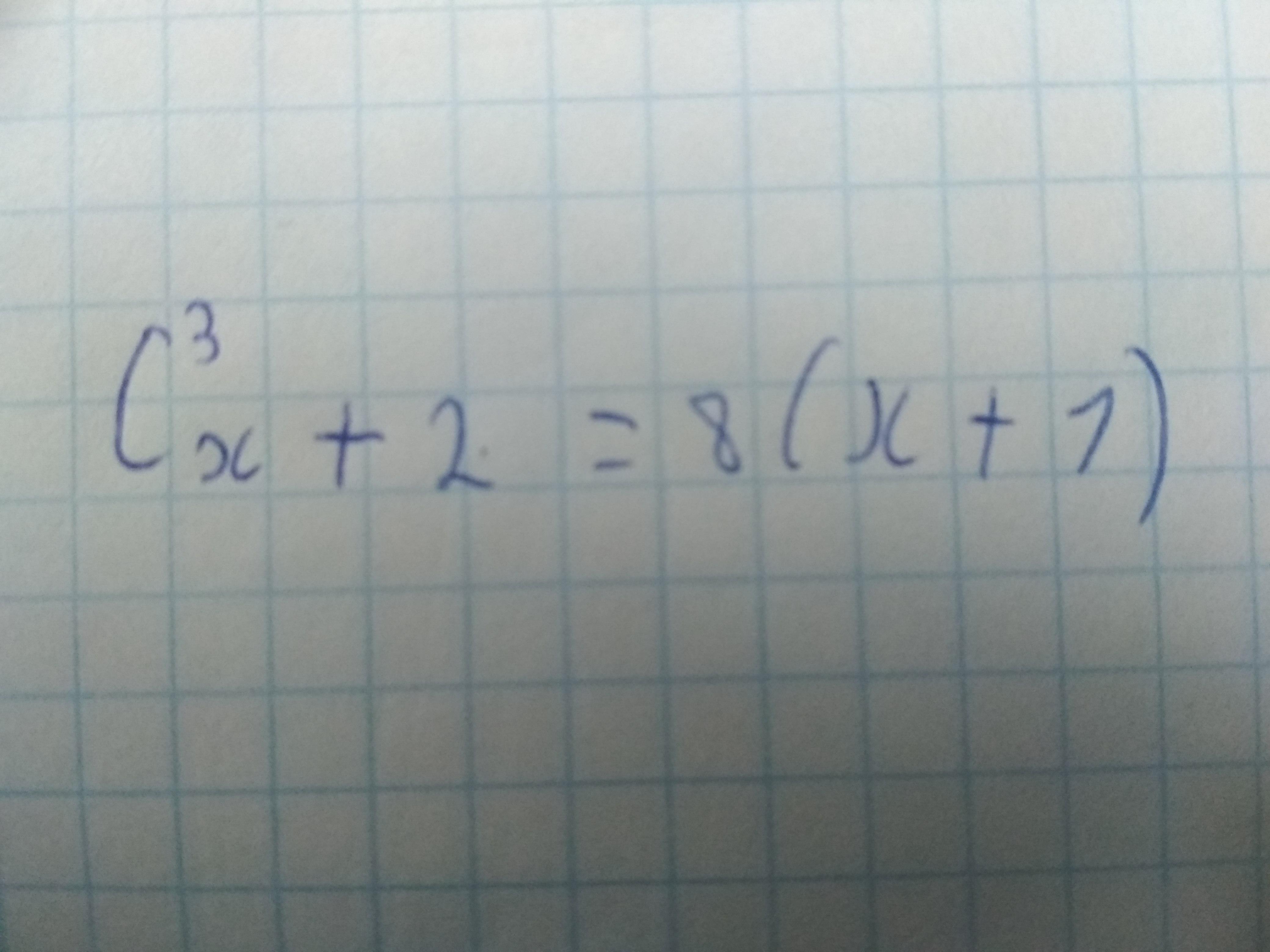
Ответы
Автор ответа:
1
Решение.
Формула: .
Ответ: х=6 .
Похожие вопросы
Предмет: Химия,
автор: kseniaslahta
Предмет: Алгебра,
автор: kissvqw
Предмет: Математика,
автор: jopykus229
Предмет: Окружающий мир,
автор: kolbasova2012