Question

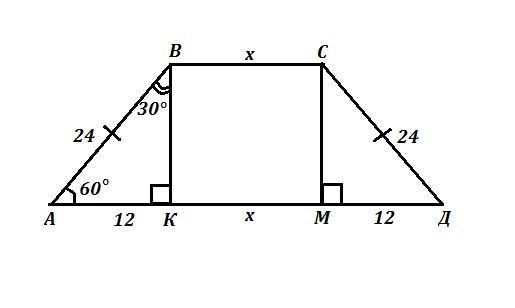
6. У рівнобічній трапецiï один з кутів 60º, бiчна сторона дорівнює 24 см, а сума основ - 44 см. Знайти середню лінію трапеції та її основи. ​

Answer 1

Решение.

АВСД - равнобокая трапеция , АВ=СД=24 см , ВС+АД=44 см , ∠А=60°

Найти среднюю линию m  и основания трапеции  ВС , АД .

 Средняя линия трапеции равна полусумме её оснований , то есть

$\bf m=\dfrac{BC+AD}{2}=\dfrac{44}{2}=22$  см

Проведём две высоты трапеции  ВК  и  СМ  к основанию АД .

Рассмотрим ΔАВК и  ΔДСМ  .

ВК=СМ  как высоты трапеции , проведённые к одному основанию .

∠А=∠Д=60° , так как трапеция равнобедренная    ⇒ ∠АВК=∠ДСМ=30°

ΔАВК=ΔСМД   по 1 признаку равенства треугольников (АВ=СД , ВК=СМ , ∠АВК=∠ДСМ)  ⇒   ΔАВК=ΔДСМ   ⇒  АК=ДМ

Катет, лежащий против угла в 30° равен половине гипотенузы, поэтому   АК=ДМ=24:2=12 см .

Обозначим  х=КМ=ВС  ( равенство сторон вследствие того, что ВСМЕ - прямоугольник) .

АД=АК+КМ+МД=12+х+12=24+х

Средняя линия треугольника  

$\bf m=\dfrac{\bf (24+x)+x}{2}=\dfrac{24+2x}{2}=12+x\ \ ,\ \ \bf 12+x=22\ \ \to \ \ x=10$  

Основания трапеции равны

ВС = х = 10 см

АД = 24+х = 24+10 = 34 см

Ответ:  m=22 см  ,  ВС=10 см ,  АД=34 см .