Question

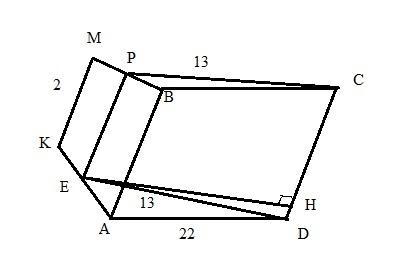
Квадрат ABCD і трапеція АВМК (АВ || МК) лежить у різних площинах.
Точки E iP - середини відрізків AK і MB відповідно. AD = 22см, КМ = 2см,
DE-CP-13см. Виконайте малюнок. Запишіть на малюнку всі вiдомi довжини.
1) Визначте вид чотирикутника CDEP.
2) Знайдіть EP.
3) Обчисліть висоту чотирикутника CDEP.
4) Обчисліть площу чотирикутника CDEP.

Answer 1

Ответ:

Пошаговое объяснение:

Точки Е и Р - середины отрезков АК и МВ, значит ЕР - средняя линия трапеции, и EP || AB. В то же время, ABCD - квадрат, значит CD || AB => EP || CD (две прямые, параллельные третьей, параллельны между собой). При этом ЕР не равно CD, а ED не параллельно CP, а значит четырехугольник CDEP - не параллелограмм, а равнобедренная трапеция (поскольку по условию ED=CP). (1)

2) ЕР=(КМ+АВ)/2=(2+22)/2=12 см

3) Высота равнобедренной трапеции вычисляется по формуле:

EH=1/2*√(4*ED²-(CD-EP)²)=1/2*√(4*13²-(22-12)²)=12 см

4) S(CDEP)=1/2*(CD+EP)*EH=1/2*(22+12)*12=204 см²