Предмет: Математика,
автор: whenweintev
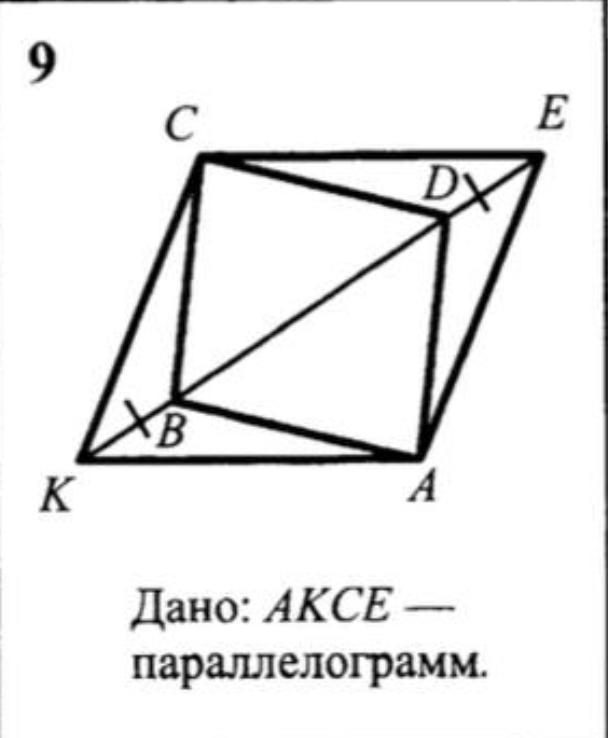
Помогите пожалуйста, нужно доказать, что ABCD - параллелограмм.
Приложения:
Ответы
Автор ответа:
2
Ответ:
Пошаговое объяснение:
1) Рассмотрим △CBK и △ADE. У них ∠CKB=∠AED, как накрест лежащие при CK || AE. CK=AE, т.к. AKCE - параллелограмм, BK=DE по условию задачи (рисунка). Значит △CBK=△ADE по 1му признаку. => BC=DA.
2) Рассмотрим △ABK и △CDE. У них ∠AKB=∠CED, как накрест лежащие при CE || KA. CE=KA, т.к. AKCE - параллелограмм, BK=DE по условию задачи (рисунка). Значит △ABK=△CDE по 1му признаку. => AB=CD.
Сопоставляя 1) и 2), делаем вывод, что ABCD - параллелограмм, поскольку у него противоположные стороны попарно равны между собой.
whenweintev:
спасибо вам большое!
Похожие вопросы
Предмет: Физика,
автор: wabadabym2234
Предмет: Литература,
автор: n61081198
Предмет: История,
автор: PonChikqq
Предмет: Литература,
автор: aftershock416
Предмет: Немецкий язык,
автор: csaffawe