Question

Доведіть, що середня лінія описаної рівнобедреної трапеції дорівнює
бічній стороні.

Answer 1

Ответ:

Доказано, что средняя линия трапеции равна боковой стороне.

Объяснение:

Докажите, что средняя линия описанной равнобедренной трапеции равна боковой стороне.

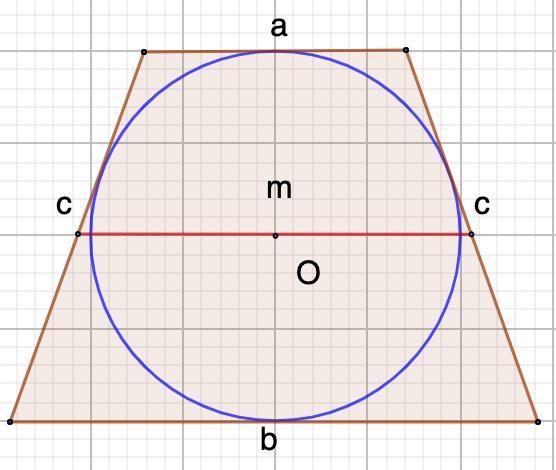
Дано: равнобедренная трапеция;

Окр.О - вписана;

m - средняя линия.

Доказать: m равна боковой стороне.

Доказательство:

Пусть основания трапеции равны а и b, а боковые стороны равны с.

• В четырехугольник можно вписать окружность, если суммы противоположных сторон равны.

⇒ a + b = 2c     |:2

$\displaystyle \frac{a+b}{2}=c$    (1)

• Средняя линия трапеции равна полусумме оснований.

⇒  $\displaystyle m=\frac{a+b}{2}$    

Заменив в равенстве (1) левую часть на m, получим:

m = c

Доказано, что средняя линия трапеции равна боковой стороне.

#SPJ1