Помогите пожалуйста, как это решить.
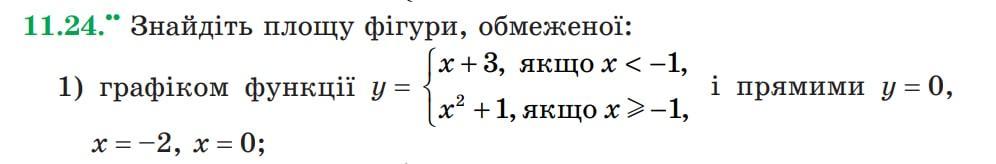
Ответы
Ответ:
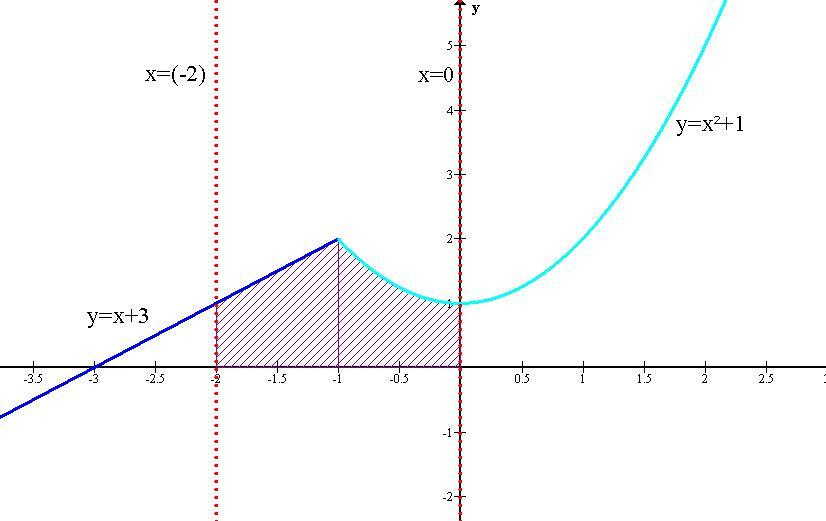
Площадь фигуры, ограниченной графиками функций y=x+3 при x ∈ (-∞; -1), y=x²+1 при x ∈ (-1; +∞), х=0, х=(-2) и у=0 равна 17/6 единиц квадратных.
Пошаговое объяснение:
Для начала нам нужно построить график. Имеем y=x+3, если x<(-1), тогда на промежутке x ∈ (-∞; -1) мы чертим график функции y=x+3; а ещё y=x²+1, если x>(-1), значит, на промежутке x ∈ (-1; +∞) мы чертим график ф-ции y=x²+1.
Файл прикреплён.
Нам нужно найти площадь заштрихованной фигуры. Предлагаю разделить нахождение этой площади на три части.
1) Находим площадь этой фигуры на промежутке (-2; -1), она будет равна значению определённого интеграла ф-ции у=х+3 от (-2) до (-1).
2) Находим площадь этой фигуры на промежутке (-1; 0), она будет равна значению определённого интеграла ф-ции у=х²+1 от (-1) до 0.
3) Находим сумму получившихся значений. Результат и будет площадью искомой фигуры.
Площадь фигуры, ограниченной графиками функций y=x+3 при x ∈ (-∞; -1), y=x²+1 при x ∈ (-1; +∞), х=0, х=(-2) и у=0 равна 17/6 единиц квадратных.