Предмет: Геометрия,
автор: bolleon1004
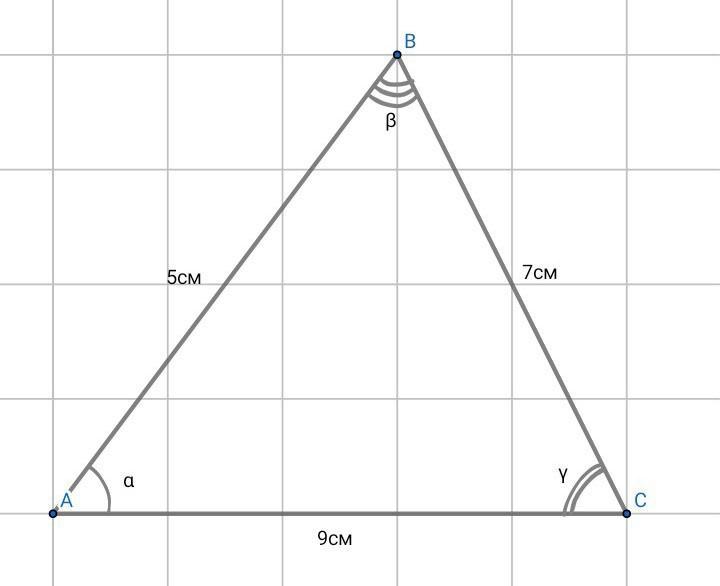
6. Розв'яжіть трикутник АВС, якщо АВ = 5 см, ВС = 7 см, АС = 9 см (кути знайдіть з точніс- тю до градусів).
Ответы
Автор ответа:
7
Ответ:
α = 51° , β = 96° , γ = 33°
Объяснение:
Дано:
∆АВС , АВ = 5 см , ВС = 7 см , АС = 9 см
Найти:
α , β , γ
Решение:
Известны 3 стороны , один из углов мы можем найти через теорему косинусов:
Где α - угол между сторонами b и с.
Таким образом:
Второй из углов тоже найдем через теорему косинусов:
Третий угол мы можем найти с учетом того , что сумма углов треугольника должно составить 180° , значит:
Приложения:
Похожие вопросы
Предмет: Физика,
автор: valikon704666
Предмет: История,
автор: maryshelestsestra
Предмет: Английский язык,
автор: mokereha
Предмет: Геометрия,
автор: noomengg