Question

СРОЧНО!!!!!ПОЖАЛУЙСТА!!!!! с рисунком!!!!
Боковое ребро правильной треугольной призмы равно 6 см, а диагональ боковой грани образует с плоскостью основания угол 30°. Найдите площадь боковой поверхности этой призмы.

Answer 1

Ответ:

Sбок = 108√3 см².

Объяснение:

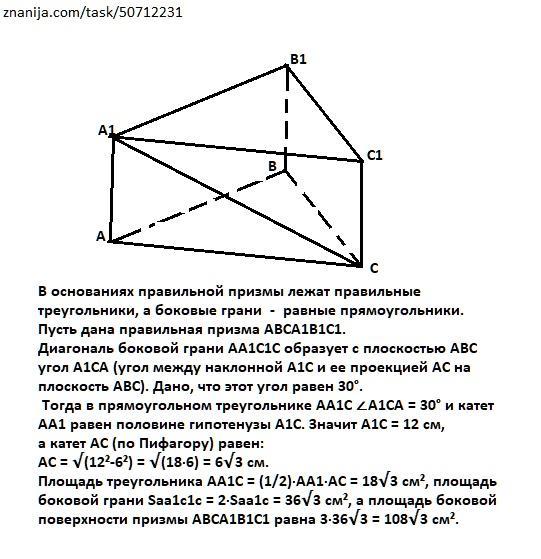
В основаниях правильной призмы лежат правильные треугольники, а боковые грани  -  равные прямоугольники.

Пусть дана правильная призма АВСА1В1С1.

Диагональ боковой грани АА1C1C образует с плоскостью АВС угол A1CA (угол между наклонной А1C и ее проекцией АC на плоскость АВС). Дано, что этот угол равен 30°.

Тогда в прямоугольном треугольнике АА1C ∠A1CA = 30° и катет АА1 равен половине гипотенузы А1C. Значит А1C = 12 см,

a катет АC (по Пифагору) равен:

AC = √(12²-6²) = √(18·6) = 6√3 см.

Площадь треугольника АА1C = (1/2)·AA1·AC = 18√3 см², площадь боковой грани Saa1c1c = 2·Saa1c = 36√3 cм², а площадь боковой поверхности призмы ABCA1B1C1 равна 3·36√3 = 108√3 см².