Предмет: Геометрия,
автор: uzasnojdana
Решите, пожалуйста данную задачу
Приложения:
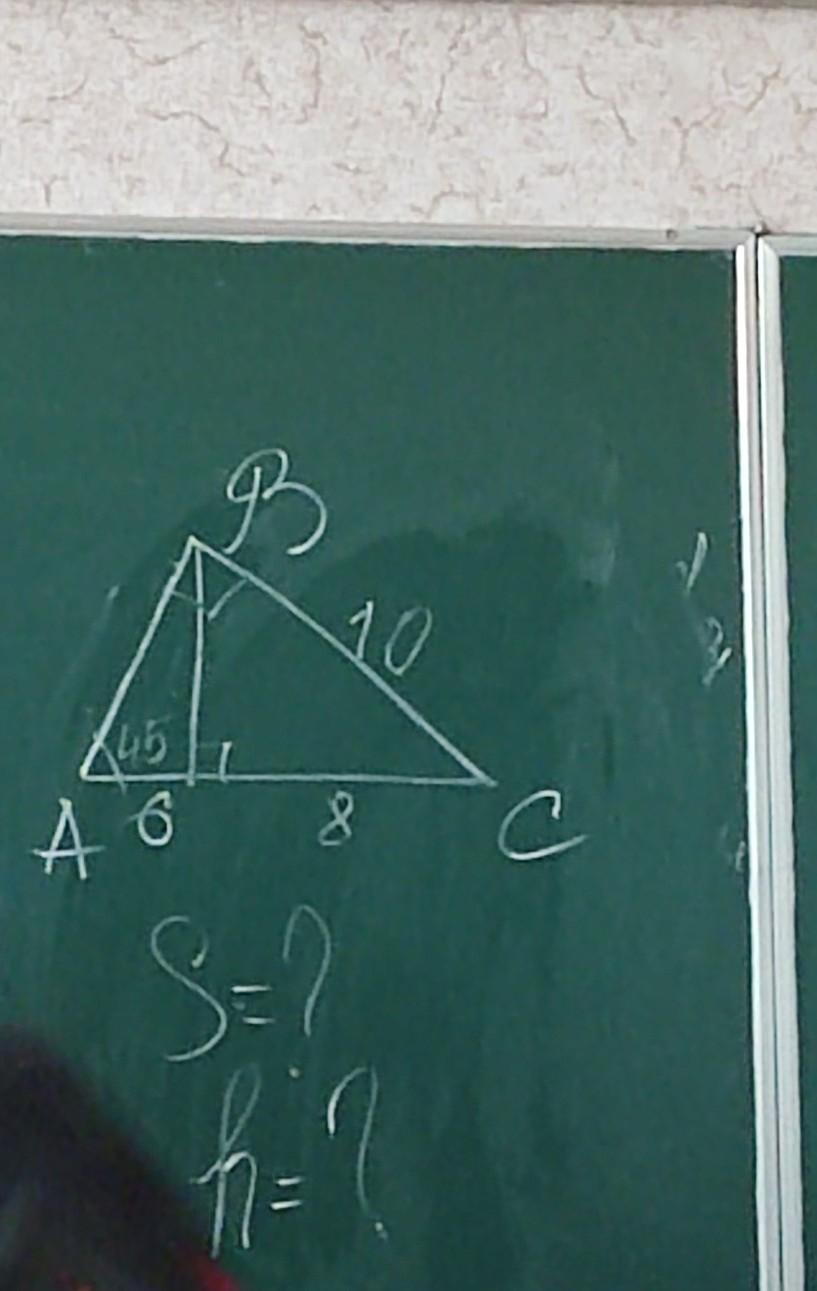
Ответы
Автор ответа:
3
Ответ: h = 6; S = 42.
Объяснение:
Пусть М это та самая точка, которая делит АС на отрезки длинами 6 и 8 см. Рассмотрим треугольник АВМ.
Угол ВМА прямой, значит угол АВМ равен 180 - (90+45)=45 градусов. Следовательно, стороны ВМ и АМ равны. Это гласит о том, что помимо того, что треугольник АВМ прямоугольный, он еще и является равнобедренным. Значит, АМ = ВМ = 6 см.
Используя значение этой высоты, находим площадь:
uzasnojdana:
Здравствуйте, есть возможность решать без корней. Мы их еще не проходили!
аа ок. попробую как-нибудь по-другому )
все, написал
А ДА ЗАБЫЛ. Мы остановились на теме Площади треугольника, но Пифагора и корни мы не проходили! Мы писали такие формулы: S=ah/2(треугольник), S=1/2 ab(прямоугольный треугольник), S1/S2=h1/h2, S1/S2=a1/a2
Спасибо
Здравствуйте. Простите, что потревожил. Объясните мне, пожалуйста. AМ=BM из-за свойства равнобедренного треугольника? Угол В 45° и угол А 45°, значит треугольник равнобедренный и из-за свойства боковые стороны тоже равны?
Да, правильно. Углы А и В равны 45 градусам, значит треугольник АВМ равнобедренный. А так как треугольник равнобедренный, боковые стороны равны
СПАСИБО ВАМ БОЛЬШОЕ, Я ИЗ-ЗА ВАС ПОНЯЛ ТЕМУ В ГЕОМЕТРИИ. ЮХУУУК
ну что ж, рад
Похожие вопросы
Предмет: Английский язык,
автор: Аноним
Предмет: Право,
автор: matvij810
Предмет: Математика,
автор: shahnozan94
Предмет: Английский язык,
автор: ander2321
Предмет: Алгебра,
автор: nataliparhomenko1977