Question

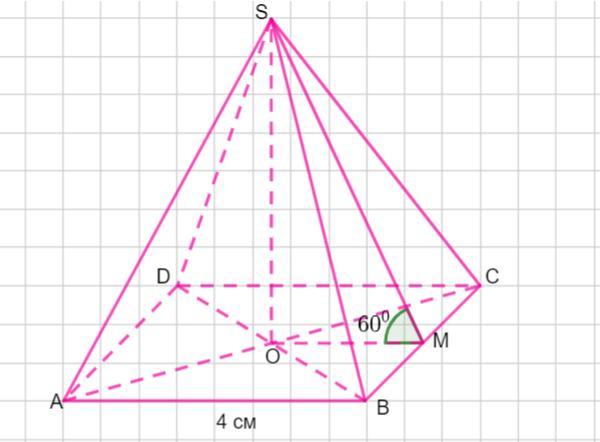
Сторона основи правильної чотирикутної піраміди дорівнює 4 см, а апофема утворює з площиною основи кут 60°. Знайдіть площу бічної поверхні піраміди.

Answer 1

Ответ:

Площадь боковой поверхности равна 32 см ².

Объяснение:

Сторона основания правильной четырехугольной пирамиды равна 4 см, а апофема образует с плоскостью основания угол 60°. Найти площадь боковой поверхности пирамиды.

Пусть дана правильная четырехугольная пирамида SABCD.

ABCD -квадрат, АВ =ВС =СD =АD= 4 см

Высота боковой грани правильной пирамиды называется апофемой.

SM- апофема, SO- высота , ∠ SMO = 60°.

Рассмотрим ΔSOM - прямоугольный .

$OM =\dfrac{1}{2} \cdot AB ;\\\\OM =\dfrac{1}{2} \cdot 4=2$  см

Косинусом острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе.

$\cos 60^{0} =\dfrac{OM }{SM} ;\\\\\dfrac{1}{2} =\dfrac{2}{SM} ;\\\\SM =4$

Значит, апофема равна 4 см.

Площадь боковой поверхности правильной пирамиды равна полупроизведению периметра основания на апофему.

Найдем периметр квадрата по формуле

$P= 4a,$

где а -сторона квадрата

$P=4\cdot4 =16$ см.

Тогда площадь боковой поверхности

$S =\dfrac{1}{2} \cdot 16\cdot 4 =8\cdot 4 =32$

Значит, площадь боковой поверхности равна 32 см ².

#SPJ1