Question

У циліндрі проведено переріз площиною, паралельною до осі циліндра. Відстань від осі циліндра до перерізу дорівнює 8 см, а радіус циліндра дорівнює 10 см. Знайдіть площу перерізу циліндра, паралельного площині основи.

Answer 1

Ответ:

Площа перерізу циліндра, паралельного площині основи дорівнює 100π см²

Объяснение:

У циліндрі проведено переріз площиною, паралельною до осі циліндра. Відстань від осі циліндра до перерізу дорівнює 8 см, а радіус циліндра дорівнює 10 см. Знайдіть площу перерізу циліндра, паралельного площині основи.

• Циліндром називають тіло, утворене внаслідок обертання прямокутника навколо його сторони.

Циліндр складається із двох кругів, які лежать у паралельних площинах, і бічної поверхні. Круги називають основами циліндра, їх радіуси – радіусом циліндра.

• Переріз циліндра площиною, паралельною до його основи, є кругом, який дорівнює основам циліндра.

Площа основи циліндра (площа круга) обчислюється за формулою:

S=π•R²

РІШЕННЯ

Уважно читаємо умову завдання.

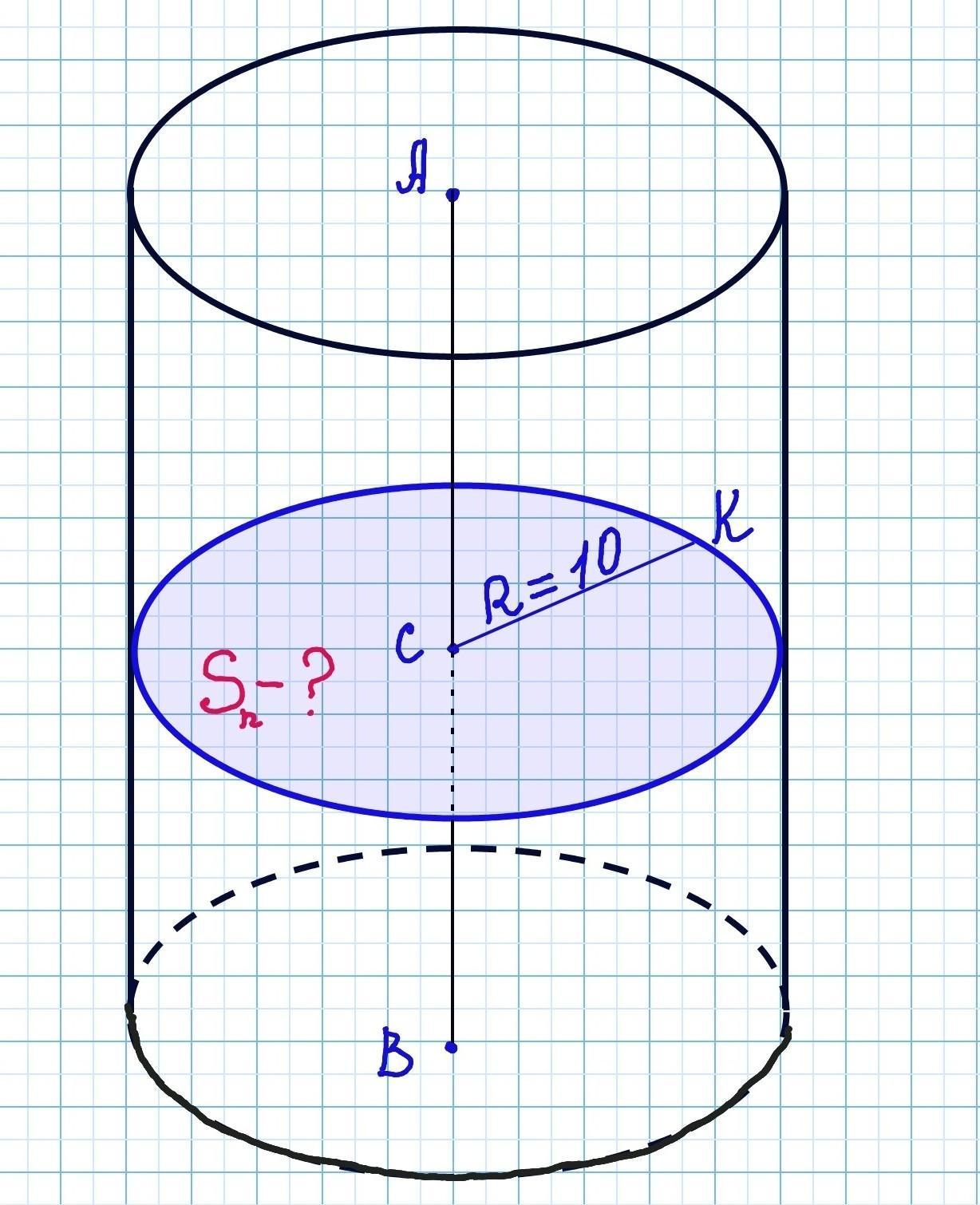
Маємо циліндр з радіусом R=10 см. Пряма AB - вісь циліндра. Точка С ∈ AB. Через точку С проведемо переріз площиною, яка є  паралельною до площини основ.

Маємо круг, який дорівнює основам циліндра.

Радіус перерізу СК дорівнює радіусу ціліндра R=10 см.

Решта умов завдання є зайвими.

Треба знайти площу перерізу циліндра, паралельного площині основи.

S=π•R²= π•10²= 100π (см²)

Відповідь: 100π см²

#SPJ1