Точка В движется в плоскости ху. Закон движения точки задан уравнениями х=f1(t)=2-t, у=f2(t)=1-t², где х и у выражены в сантиметрах, t – в секундах.
Найти уравнение траектории точки; для момента времени t =2с определить скорость и ускорение точки, а также ее касательное и нормальное ускорения и радиус кривизны в соответствующей точки траектории.
Ответы
начальная точка по оси х равна хо=3sin0-2=-2 cm
по оси у: уо=9сos0+5=9+5=14 cm
в эту же точку(-2;14) тело вернется через 12 с
через одну секунду координата: х1=3sin п*1/6 - 2=3*0.5 - 2= - 0.5 cm
y1=9*cos п*1/6 +5=9*0.87+5=12.83 cm
через две секунды : x2=3sin п*2/6 - 2 =3*0.87-2=0.61 cm y=9cos п*2/6 + 5 =9*0.5+5=9.5 cm
через три секунды: x3=3sin п*3/6 - 2 = 1 cm y3=9cos п*3/6+5=5
через 6 с : х6= - 2см y6=9*(-1)+5=-4
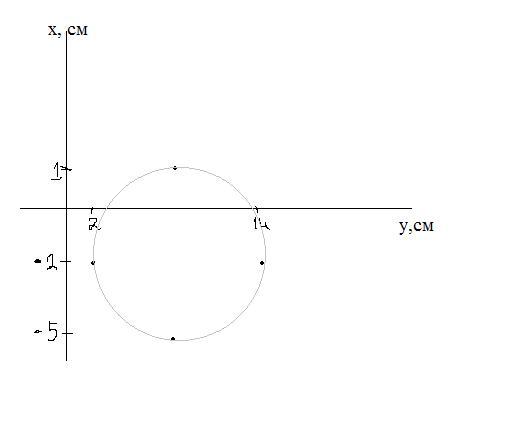
далее идет симметрично отностительно прямой x=2 (во вложениях график)
Траектория:овал (радиус по горизонтали 7 см, по вертикали 3)
скорость точки в момент времени 1с равна производной пути по оси х и оси у
vx=x"(1)=(3sin п*1/6 -2)" = 3*сos п/6 = 2.7 см/с
vy=y"(t)=(9сosп/6+5)"=9*sin п/6=4.5 см/с
по теореме пифагора v^2=vx^2+vy^2=2.7^2+4.5^2=27.54
v=5.25 см/с
ускорение в этом случае центростремительное, a=v^2/R
в момент времени 1с радиус равен R^2=(x1-xo)^2+(y1-yo)^2=(-0,5+2)^2+(12.83-14)^2=3.62
R=1.9 см
ац=5.25^2/1.9=14.5 см/с^2
в момент времени равно 0 скорость равна vx=x"(0)=3cos0=3 см/с
vy=0
тогда v=3 см/с
касательное ускорение: aк = v1-vo/t1=5.25-3/1=2.25 см/с2
нормальное ускорение : а^2=aц(0)^2+ак^2
ац(0)=vo^2/Ro=3^2/7=1.29 см/с2 - центростремит.ускорение в момент времени 0
a^2=1.29^2+2.25^2=6.73
a=2.6 см/с .