Question

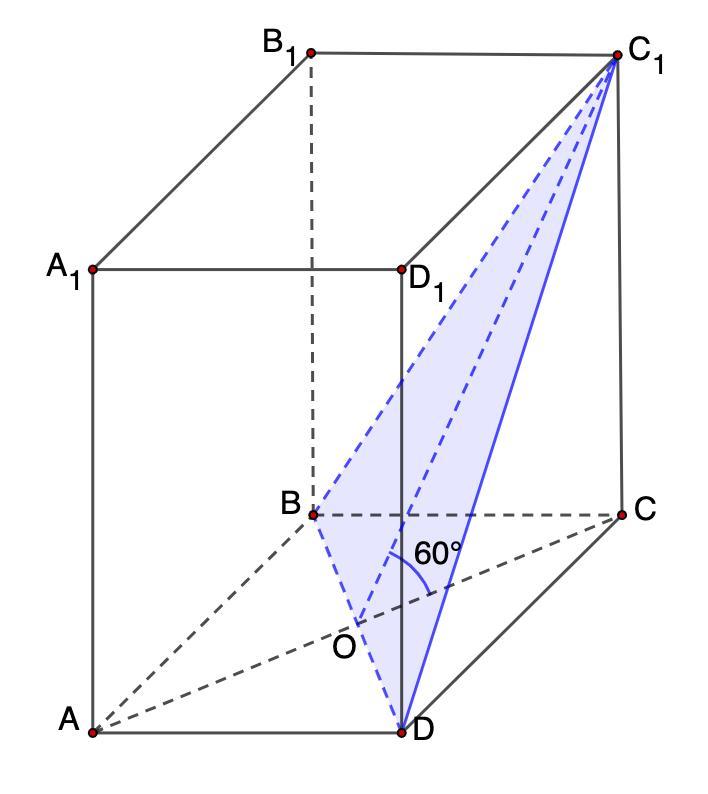
Через діагональ однієї основи правильної чотирикутної призми і вершину другої основи проведено переріз під кутом 60° до площини основи. Знайдіть площу перерізу, якщо площа основи призми дорівнює 64 см2.

Answer 1

Ответ:

Площадь сечения равна 64 см².

Объяснение:

Через диагональ одного основания правильной четырехугольной призмы и вершину второго основания проведено сечение под углом 60° к плоскости основания. Найдите площадь сечения, если площадь основания призмы равна 64 см².

Дано: ABCDA₁B₁C₁D₁ - правильная призма;

BC₁D - сечение;

сечение наклонено под углом 60° к плоскости основания;

S(ABCD) = 64 см².

Найти: S(BC₁D)

Решение:

• В основании правильной четырехугольной призмы лежит квадрат.

⇒ ABCD - квадрат.

S(ABCD) = 64 см²

• Площадь квадрата равна квадрату его стороны.

⇒ АВ = √64 = 8 (см)

• Диагонали квадрата взаимно перпендикулярны.

⇒ CO ⊥ BD.

• Прямая, проведенная на плоскости через основание наклонной перпендикулярно ее проекции, перпендикулярна и самой наклонной.

⇒ CO ⊥ BD.

∠С₁ОС = 60° - линейный угол двугранного угла между плоскостью сечения и основанием призмы.

Рассмотрим ΔABD - прямоугольный.

По теореме Пифагора:

BD² = AB² + AD² = 64 + 64 = 128

BD = √128 = 8√2 (см)

• Диагонали квадрата равны и точкой пересечения делятся пополам.

⇒ BD = AC=8√2 см; АО = ОС = 4√2 (см).

Рассмотрим ΔОС₁С - прямоугольный.

• Косинус угла - отношение прилежащего катета к гипотенузе.

$\displaystyle cos\;60^0=\frac{OC}{OC_1} \\\\OC_1=\frac{OC}{cos\;60^0} =\frac{4\sqrt{2} }{0,5}=8\sqrt{2}$  (см)

Рассмотрим ΔBC₁D.

• Площадь треугольника равна половине произведения стороны на высоту, проведенную к этой стороне.

$\displaystyle S(BC_1D)=\frac{1}{2}\cdot BD\cdot OC_1=\frac{1}{2}\cdot 8\sqrt{2}\cdot 8\sqrt{2} =64$  (см²)

Площадь сечения равна 64 см².

#SPJ1