Предмет: Алгебра,
автор: sakyrasw
можете расписать по дискриминанту и виета пожалуйста, по простому но понятно
Приложения:
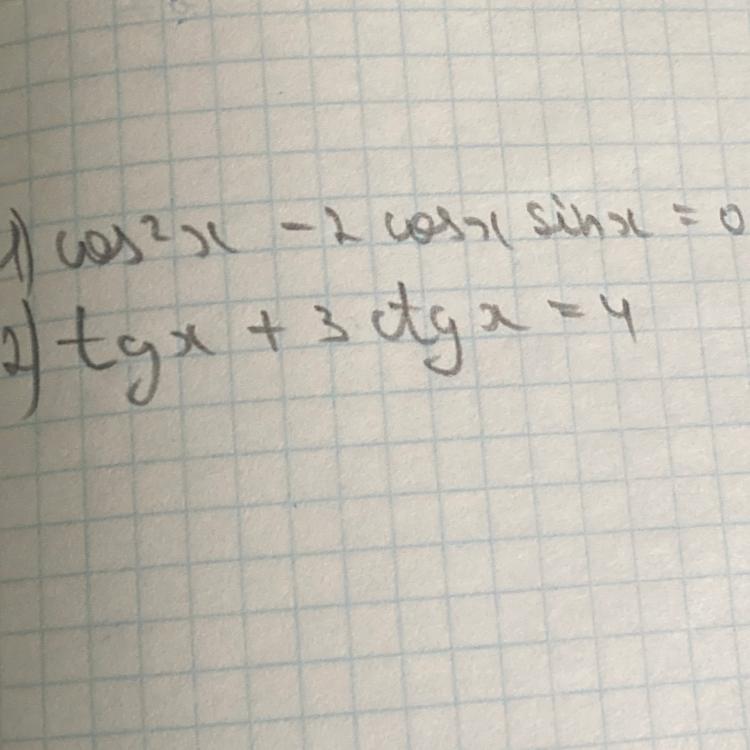
Ответы
Автор ответа:
0
Решение.
Выносим общий множитель за скобку .
Произведение равно 0 , когда хотя бы один из множителей равен 0 .
Похожие вопросы
Предмет: История,
автор: krivcacnatala
Предмет: Українська мова,
автор: bogksdhuw
Предмет: Биология,
автор: kseniadogar01
Предмет: Математика,
автор: Ameliya0009