Предмет: Алгебра,
автор: sakyrasw
ПОМОГИТЕ решить пожалуйстааааа очень срочно подробно
Приложения:
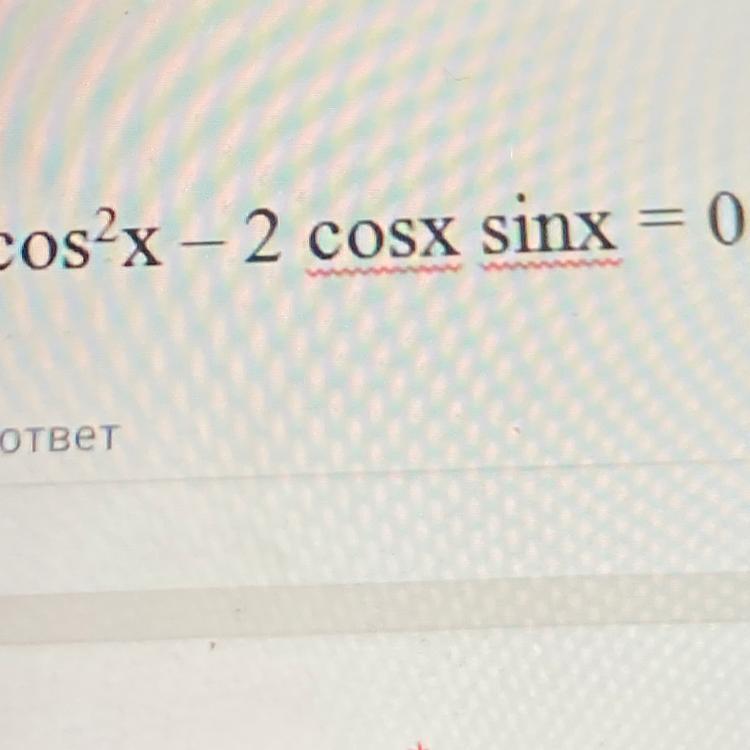
Ответы
Автор ответа:
1
Автор ответа:
1
Объяснение:
cos²x-2cosxsinx=0
cosx(cosx-2sinx)=0
cosx=0 x=π/2+kπ,k∈z
cosx-2sinx=0
-2sinx= -cosx
-2tgx= -1
tgx=1/2
x=arctg(1/2)+kπ,k∈z
решение: х=π/2+kπ,k∈z
x=arctg(1/2)+kπ,k∈z
Похожие вопросы
Предмет: Алгебра,
автор: lolliinna
Предмет: Биология,
автор: artemvetrov1810
Предмет: Алгебра,
автор: asylbekaltaiuly
Предмет: Русский язык,
автор: maratismakov02
Предмет: История,
автор: Аноним