Question

Діагональ осьового перерізу циліндра дорівнює 2 корінь з 5 см. знайдіть висоту циліндра якщо його радіус дорівнює 1 см

Answer 1

Ответ:

Висота циліндра дорівнює 4 см

Объяснение:

Діагональ осьового перерізу циліндра дорівнює 2 корінь з 5 см. Знайдіть висоту циліндра якщо його радіус дорівнює 1 см

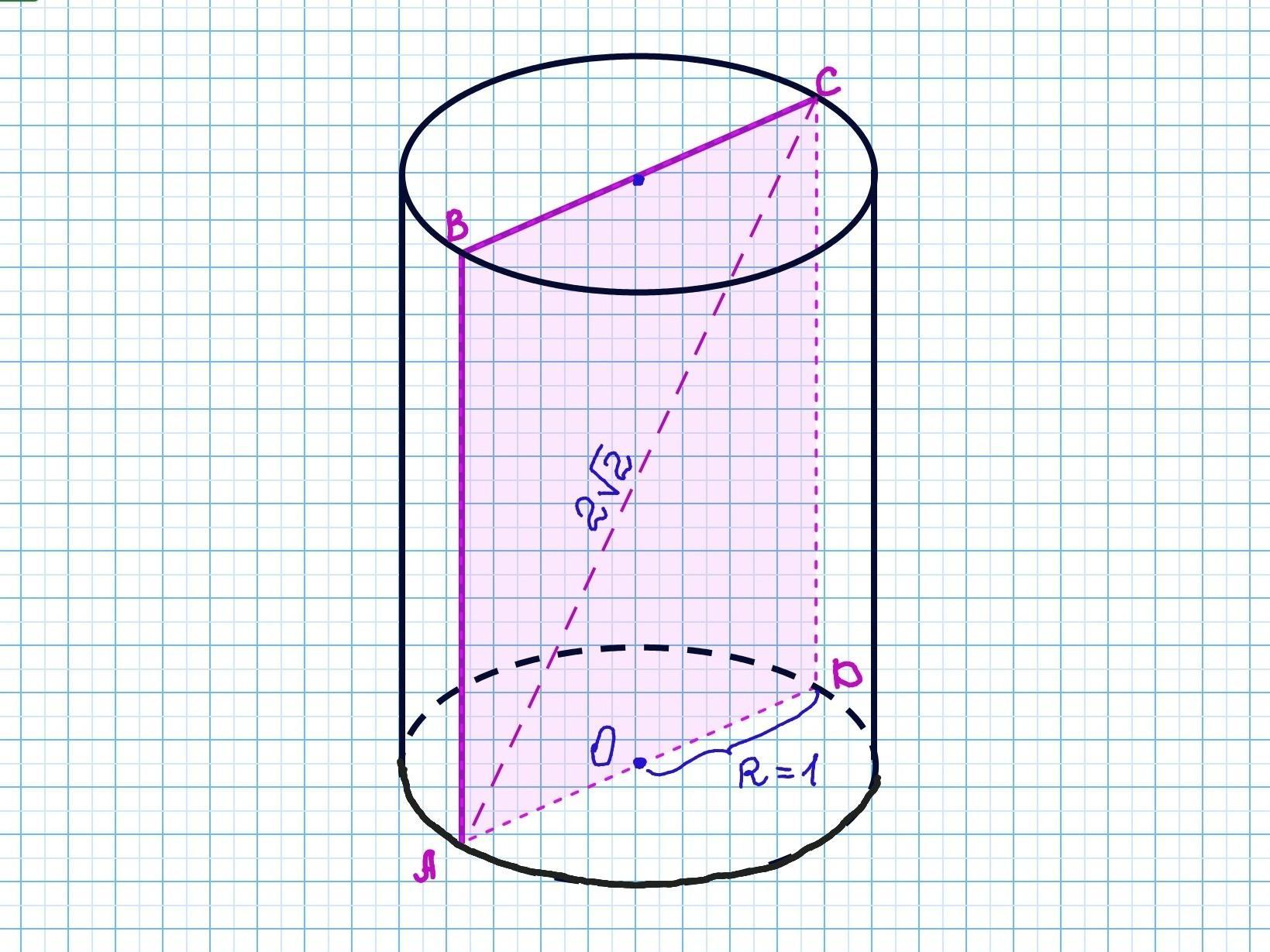
Маємо циліндр з радіусом R=1 см і його осьовий переріз - прямокутник ABCD. Сторони BC і AD - діаметри основи кола. AD=BC=2•R=2•1= 2 см. Сторони CD і AB є твірними циліндра (їх довжина дорівнює висоті циліндра). Діагональ особового перерізу - діагональ прямокутника AC = 2√5 см.

Оскільки циліндр прямий, то CD⟂AD (висота перпендікулярна до діаметра).

Із прямокутного трикутника ACD (∠D=90°) в якому AC - гіпотенуза, AD - катет, за теоремою Піфагора знайдемо катет CD - висоту циліндра:

CD²= AC²-AC²

CD²=(2√5)²-2²=20-4=16

CD =√16= 4 см

Відповідь: Висота циліндра дорівнює 4 см

#SPJ1