Предмет: Математика,
автор: lolkino158
Вычислить первые 4 интегралла 30 балов плачу
Приложения:
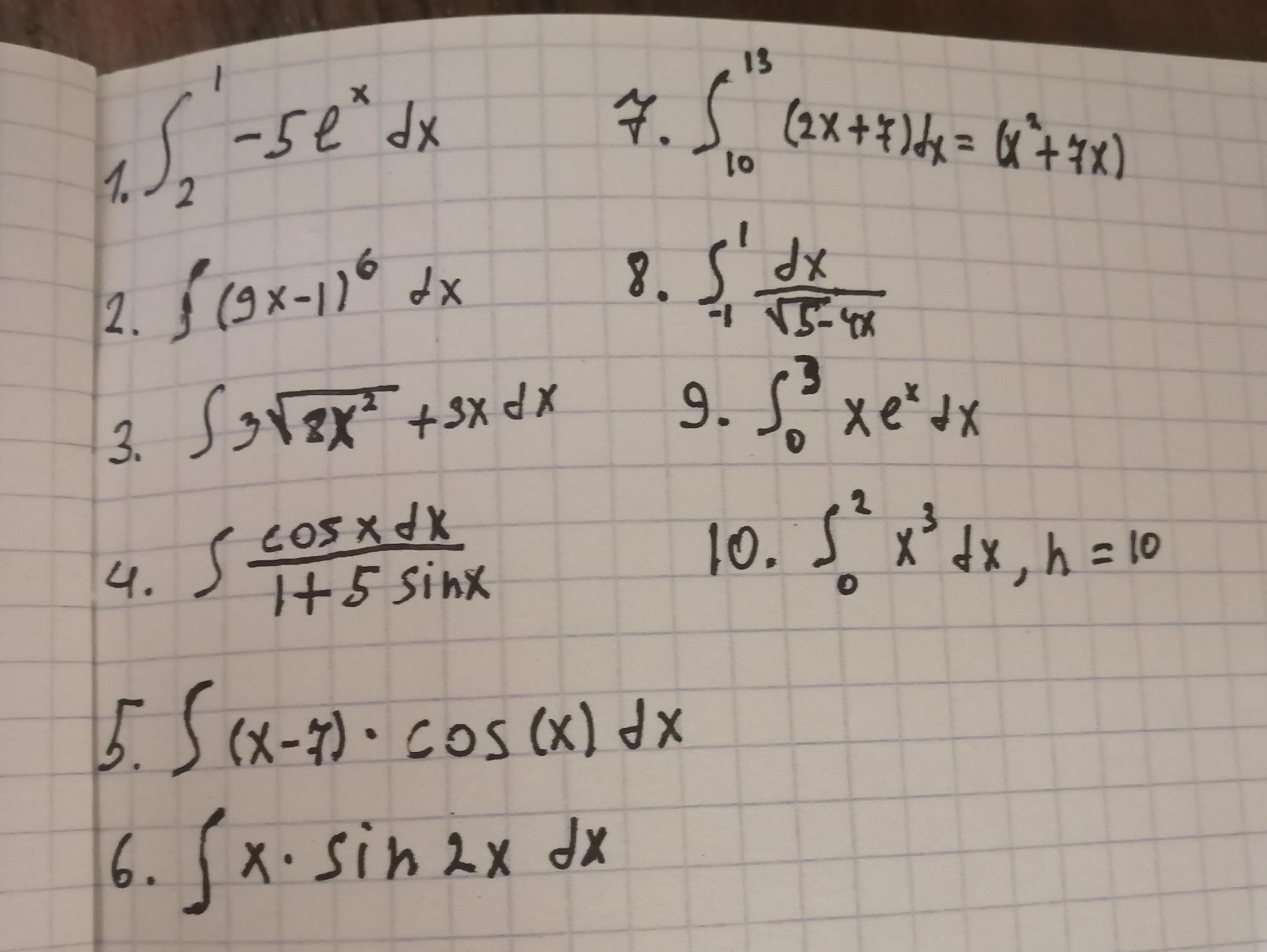
Ответы
Автор ответа:
0
Ответ: 1.
2.
3.
4.
Решение с объяснением:
1. Применим свойство интеграла перестановки местами пределов:
2. Дифференциал приводим к виду выражения в скобках и интегрируем по степени:
3. Применим свойство алгебраической суммы и интегрируем два интеграла:
4. Дифференциал приводим к виду выражения в знаменателе:
Похожие вопросы
Предмет: Геометрия,
автор: mis77777
Предмет: Геометрия,
автор: balanukinna461
Предмет: Математика,
автор: kotenok201888
Предмет: География,
автор: babaycalat
Предмет: География,
автор: hacma52