Предмет: Алгебра,
автор: jjjtt
помогите пожалуйста даю 50 баллов
ПОЖАЛУЙСТА кто нибудь
Приложения:
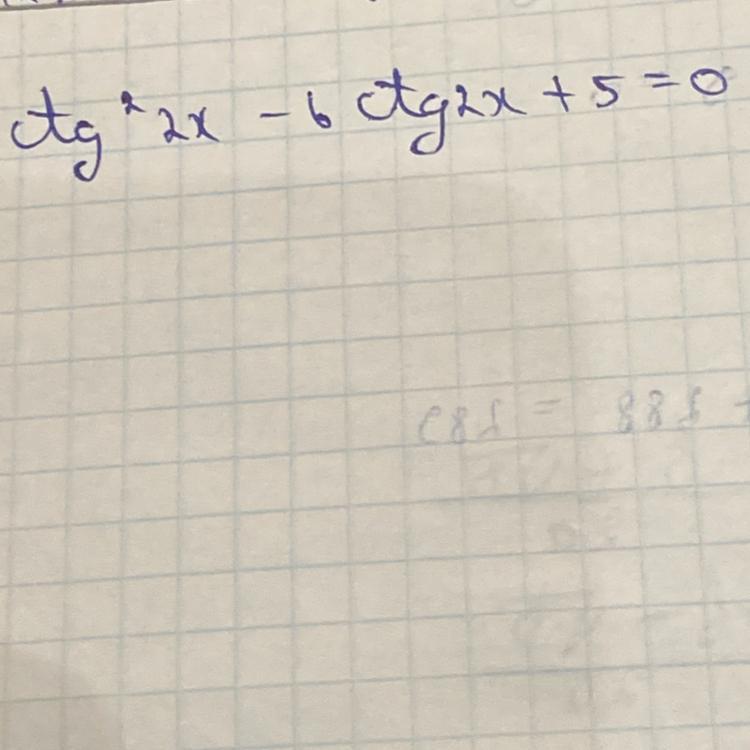
Ответы
Автор ответа:
2
Ответ:
Объяснение:
ctg² 2x - 6ctg 2x + 5 =0
Введем замену
ctg 2x = t , ctg²2x = t²
t² -6t + 5= 0
( t - 1 )(t -5) =0
t₁ = 1 , t₂ = 5
Таким образом
1)ctg 2x = 1
2x = arcсtg(1) + πn
2)ctg2x = 5
2x = arcctg(5) + πn
Похожие вопросы
Предмет: Английский язык,
автор: Аноним
Предмет: Математика,
автор: lenapavkina174
Предмет: Русский язык,
автор: mytkonazar2
Предмет: Қазақ тiлi,
автор: fvrav99