Предмет: Алгебра,
автор: TheAlexFunny
Пределы функции. Второй замечательный предел.
Приложения:
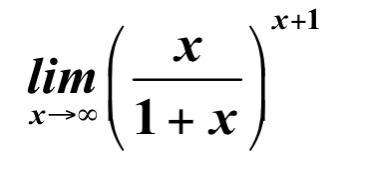
Ответы
Автор ответа:
1
Ответ: 1/e
Объяснение:
Выражение, стоящее под лимитом, приводим к такому виду, чтобы оно соответствовало второму замечательному пределу:
.
Похожие вопросы
Предмет: Химия,
автор: Аноним
Предмет: Английский язык,
автор: yusifchalabii
Предмет: Математика,
автор: Bonia00
Предмет: Литература,
автор: 100yaroslav100
Предмет: Алгебра,
автор: old77