знайти координати центру ваги представленої нижче плоскої фігури.
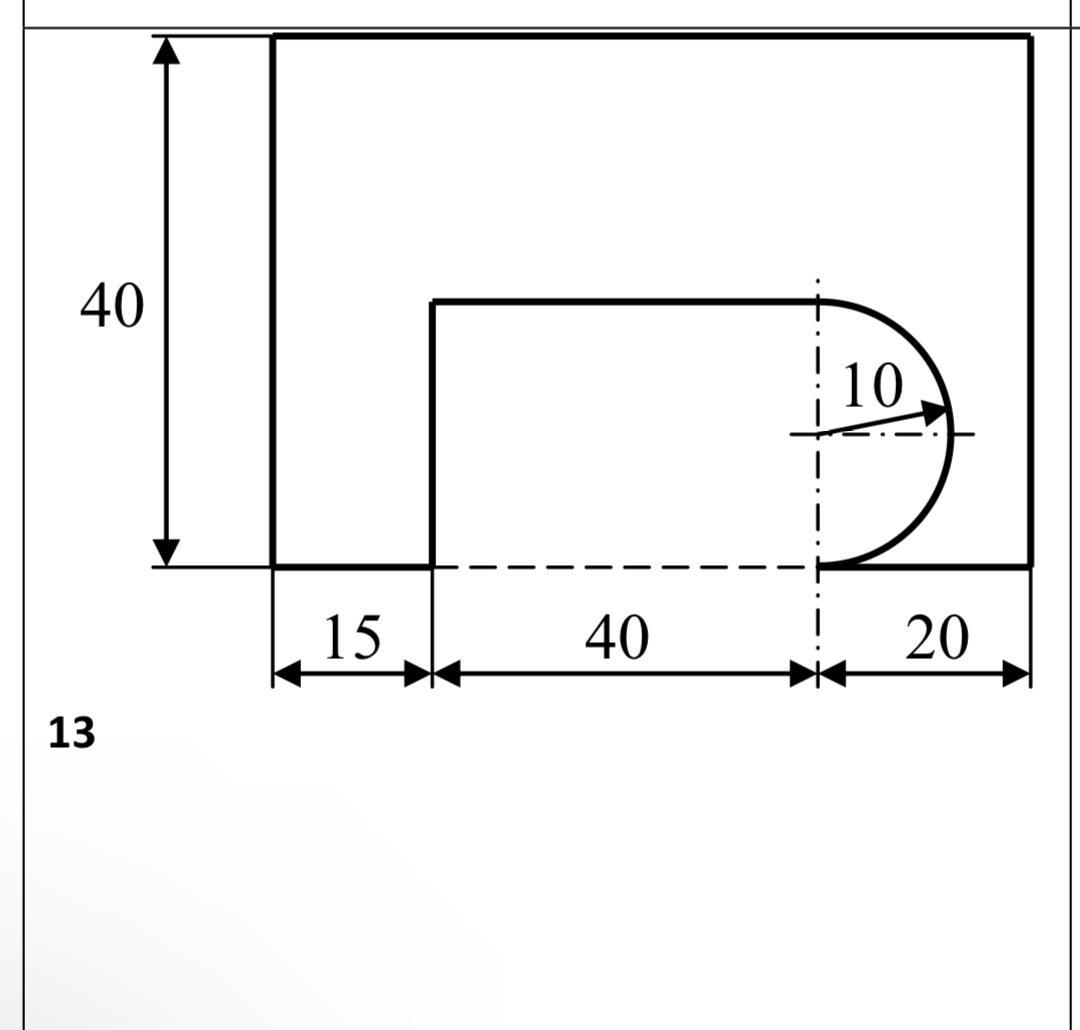
Ответы
Формулы для определения положения центра тяжести различных тел имеют вид:
xc = (∑ Gixi) / ∑ Gi;
yc = (∑ Giyi) / ∑ Gi;
Для плоских фигур массу G заменяем на площадь S.
Для полукруга хс = 4R/(3π) = 4*10/(3*3,14159) ≈ 4,24413.
Для прямоугольников центр тяжести находится на пересечении диагоналей.
Подставим данные: S*x/S*y
x = 75 S= 3000 x/2 = 37,5 112500
y = 40 y/2 = 20 60000
x = 40 S= -800 x/2 = 20 35 -28000
y = 20 y/2 = 10 10 -8000
xo = 55 S= -157,08 хц = 4,244132 59,24413 -9306,05
yo = 10 уц = 10 10 -1570,8
∑(S) = 2042,92 ∑Sx = 75193,95
∑Sy= 50429,2
Ответ: х(цт) = 75193,95/2042,92 = 36,80709
у(цт) = 50429,2/2042,92 = 24,68486