Question

Постройте график функции y=(x²-x-2)÷|x+1| с объяснением

Answer 1

Ответ:

График построен.

Объяснение:

Построить график функции

$\displaystyle y=\frac{x^2-x-2}{|x+1|}$

Во-первых, ОДЗ: х ≠ -1

Разложим числитель на множители:

$\displaystyle D=1+8 = 9;\;\;\;\;\;\sqrt{D}=3\\ \\x_1=\frac{1+3}{2}=2;\;\;\;\;\;x_2=\frac{1-3}{2}=-1\\ \\ x^2-x-2=(x-2)(x+1)$

Если подмодульное выражение положительно, то есть при х > -1, то наша функция будет иметь вид:

$\displaystyle y=\frac{(x-2)(x+1)}{x+1} =x-2$

Если подмодульное выражение отрицательно, то есть при х < -1, тогда наша функция будет иметь вид:

$\displaystyle y=\frac{(x-2)(x+1)}{-(x+1)} =-x+2$

Можем записать данную функцию, как кусочную:

$\displaystyle y=\left \{ {{x-2,\;\;\;x > -1} \atop {-x+2,\;\;\;x < -1}} \right.$

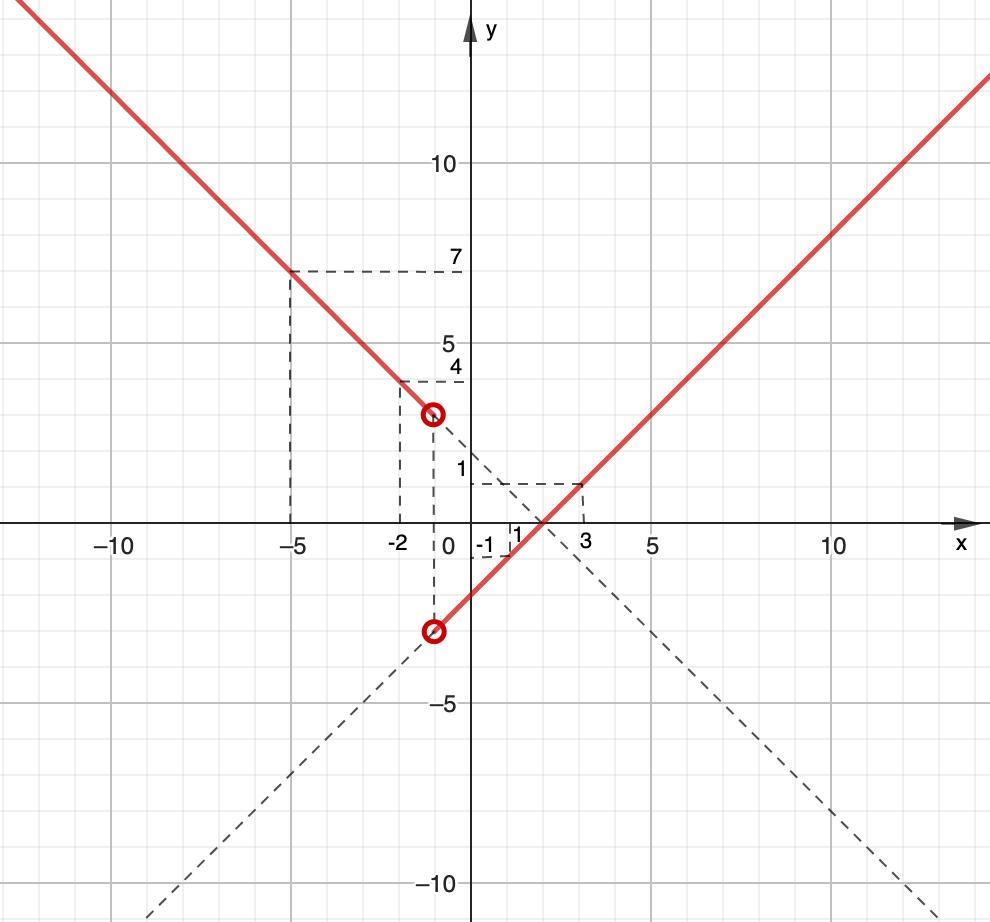
Построим график:

1. у = х - 2, если х > -1.

- линейная функция, график прямая.

$\displaystyle\arraycolsep=0.7em\begin{array}{ | c | c |c| }\cline{1-3}x& 1 & 3 \\\cline{1-3}y& -1 & 1 \\\cline{1-3}\end{array}$

Точка х = -1 - выколотая.

Так как, условие для этого графика х > -1, то берем часть графика правее этой точки.

2. у = -х + 2, если х < -1.

- линейная функция, график прямая.

$\displaystyle\arraycolsep=0.7em\begin{array}{ | c | c |c| }\cline{1-3}x& -2 & -5 \\\cline{1-3}y& 4 & 7 \\\cline{1-3}\end{array}$

Точка х = -1 - выколотая.

Так как, условие для этого графика х < -1, то берем часть графика левее этой точки.

График построен.

#SPJ1