Розв'язати нерівності (1,3,4,5,6)
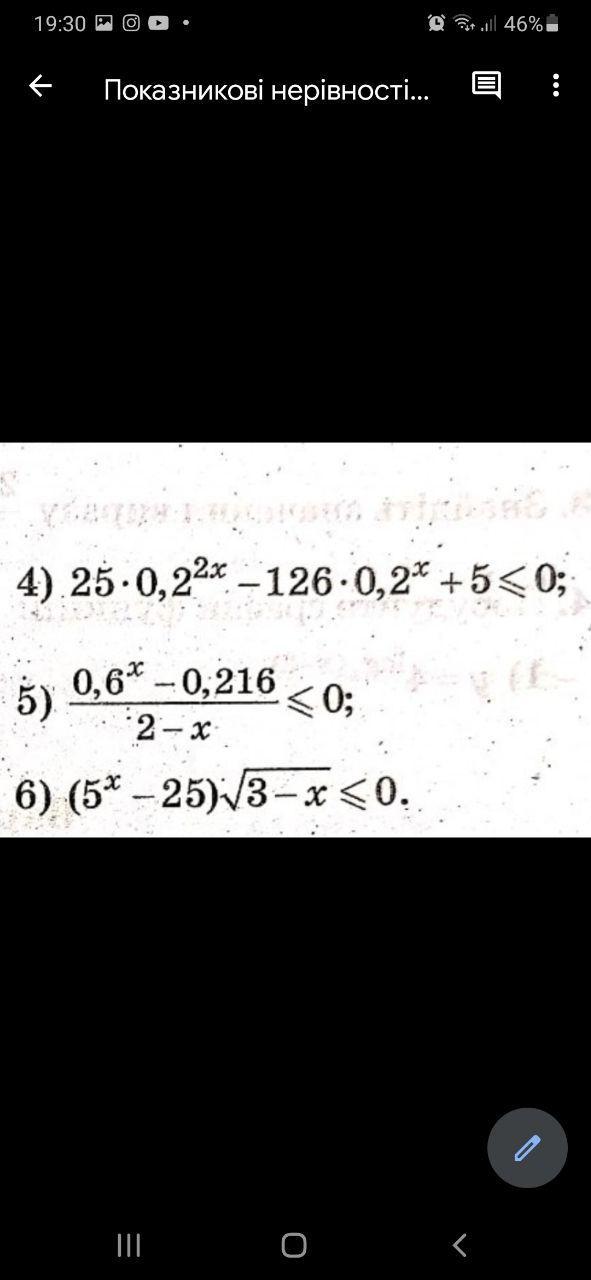
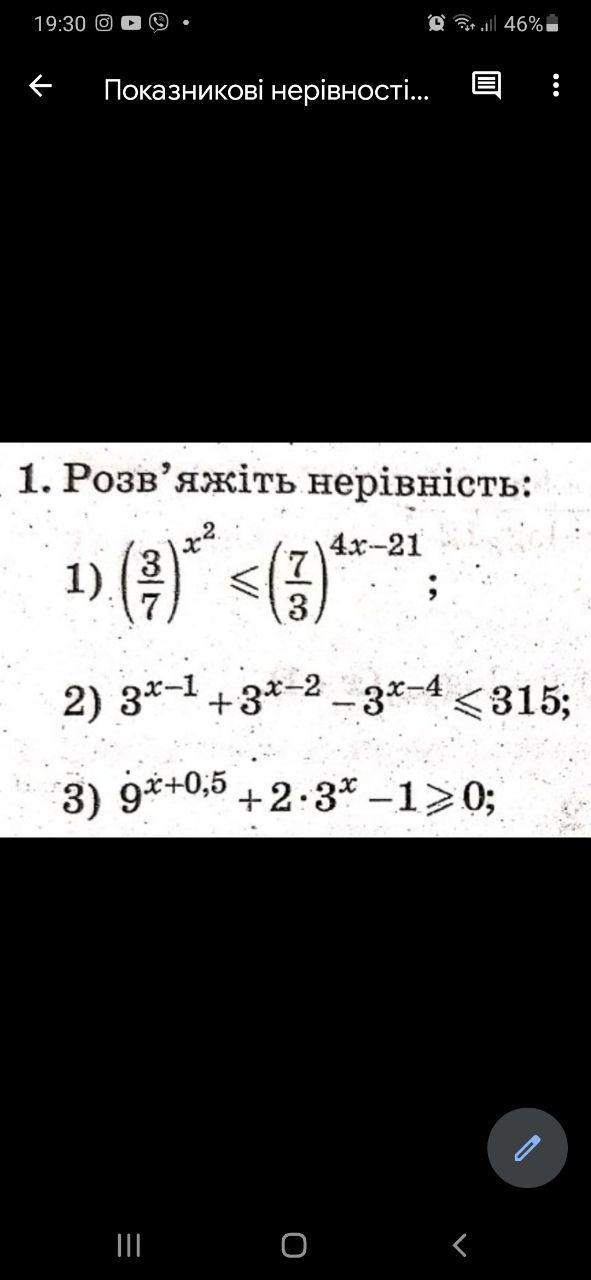
Ответы
Ответ:
Объяснение:
1) (3/7)^x²≤(7/3)⁴ˣ⁻²¹
(3/7)^x²≤(3/7)²¹⁻⁴ˣ
x²≤21-4x
x²+4x-21=0 ⇒ D=16+84=100
x₁=(-4-10)/2=-7; x₂=(-4+10)/2=3
На промежутке [-7; 3] возьмём точку 0:
(3/7)^0²≤(7/3)^(4·0-21) ⇒ 1≤(3/7)²¹- не подходит.
- + -
-----------------.--------------------.--------------------->x
-7 3
Ответ: x∈(-∞; -7]∪[3; ∞).
2) 3ˣ⁻¹+3ˣ⁻²-3ˣ⁻⁴≤315
3ˣ·(1/3 +1/9 -1/81)≤9·35
3ˣ·(27+9-1)/81≤3²·35
3ˣ·35/3⁴≤3²·35 |35
3ˣ⁻⁴≤3²
x-4≤2
x≤2+4 ⇒ x≤6
Ответ: x∈(-∞; 6].
3) 9^(x+0,5) +2·3ˣ-1≥0
3²ˣ⁺¹+2·3ˣ-1≥0
При 3²ˣ⁺¹+2·3ˣ-1=0 ⇒ 3·3²ˣ+2·3ˣ-1=0; 3ˣ=t
3t²+2t-1=0 ⇒ D=4+12=16
t₁=(-2-4)/6=-1 ⇒ 3ˣ=-1 ⇒ x=∅
t₂=(-2+4)/6=1/3 ⇒ 3ˣ=1/3 ⇒ x=-1
Возьмём точку 0:
9^(0+0,5) +2·3⁰-1≥0 ⇒ √9 +1≥0 ⇒ 4≥0
- +
--------------------------.-------------------------->x
-1
Ответ: x∈[-1; ∞).
4. 25·0,2²ˣ-126·0,2ˣ+5≤0
При 25·0,2²ˣ-126·0,2ˣ+5=0; 0,2ˣ=(1/5)ˣ=t
25t²-126t+5=0 ⇒ D=15876-500=15376
t₁=(126-124)/50=1/25 ⇒ (1/5)ˣ=1/25 ⇒ (1/5)ˣ=(1/5)² ⇒ x=2
t₂=(126+124)/50=5 ⇒ (1/5)ˣ=5 ⇒ (1/5)ˣ=(1/5)⁻¹ ⇒ x=-1
На промежутке [-1; 2] возьмём точку 0:
25·0,2^(2·0) -126·0,2⁰+5≤0 ⇒ 25-126+5≤0 ⇒ -96≤0
+ - +
------------------.-------------------.------------------>x
-1 2
Ответ: x∈[-1; 2].
5. (0,6ˣ-0,216)/(2-x)≤0 ⇒ 2-x≠0 ⇒ x≠2
При 0,6ˣ-0,216=0 ⇒ 0,6ˣ-0,6³=0 ⇒ 0,6ˣ=0,6³ ⇒ x=3.
На промежутке (-∞; 2) возьмём точку 0:
(0,6⁰-0,216)/(2-0)≤0 ⇒ 0,392≤0 - не подходит.
+ - +
-------------°--------------.---------------->x
2 3
Ответ: x∈(2; 3].
6) (5ˣ-25)√(3-x)≤0 ⇒ 3-x≥0 ⇒ x≤3 ⇒ x∈(-∞; 3].
При 5ˣ-25=0 ⇒ 5ˣ-5²=0 ⇒ 5ˣ=5² ⇒ x=2
На промежутке (-∞; 2] возьмём точку 0:
(5⁰-25)√(3-0)≤0 ⇒ -24√3≤0
- + +
-----------------.----------------------.--------------------->x
2 3
Ответ: x∈(-∞; 2]∪{3}.