Предмет: Алгебра,
автор: hdhdhhdhdhdkk
СРОЧНО!!!!
ПОЖАЛУЙСТА
Приложения:
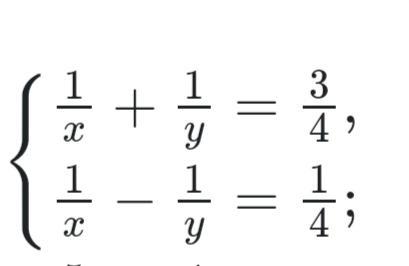
Ответы
Автор ответа:
0
Ответ:
упрощаем расчёт сделав замену t=1/x, u=1/y:
решаем систему уравнений методом "исключения неизвестных":
делим обе стороны уравнения на 2:
подсиавляем данное значение t в уравнение t-u=1/4:
решением данной системы уравнений является упорядочная пара чисел(t, u):
проверяем, верно ли данная упорядочная пара чисел решением системы уравнений:
упростим систему:
упорядочная пара чисел является решением системы уравнений, так как оба равенства верны.
подставляем значения t, u обратно в 1/x=t и 1/y=u:
решаем систему уравнений:
ну дальше надеюсь и так всё понятно.
himikomat:
отметь как лучший ответ пж
спасибо))))
Похожие вопросы
Предмет: Психология,
автор: Аноним
Предмет: История,
автор: Nolle
Предмет: Окружающий мир,
автор: agglarw
Предмет: История,
автор: turlubekovnurlyhan