Предмет: Алгебра,
автор: demanovskam
Знайдіть область визначення функції:
а) (-5;3] U [3;+∞)
б) [3;5) U (5;+∞)
в) (3;5] U [5;+∞)
г) [-3;-5) U (-5;+∞)
Дуже терміново треба не тільки відповідь, а й розв'язок. Дам 20 балів
Приложения:
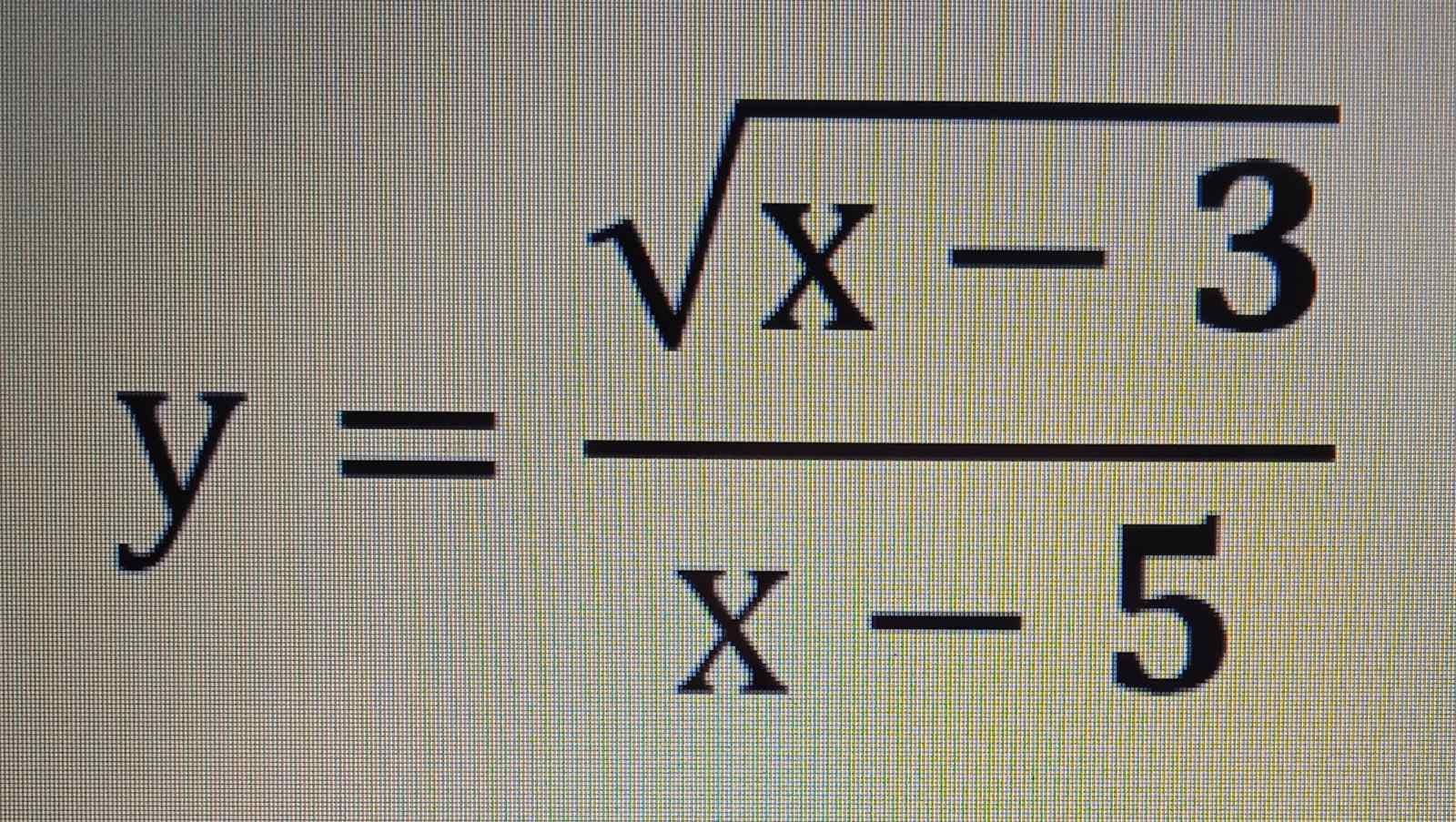
Ответы
Автор ответа:
0
Ответ:
б)
решение:
разделяем функцию на части, чтобы найти область опредления каждой части:
область определения рациональной функции:
область определения функции корня чётной степени:
область определения двух линейных функций является множесиво всех действительных чисел:
из этого получаем:
находим пересечение:
demanovskam:
Спасибо
Похожие вопросы
Предмет: Геометрия,
автор: Stenamov
Предмет: Окружающий мир,
автор: nurlanovmadi8
Предмет: Психология,
автор: Аноним
Предмет: Физика,
автор: aaaaaasifon
Предмет: Алгебра,
автор: dimashevtsov3