Предмет: Математика,
автор: Аноним
Визначити максимум і мінімум функції
Приложения:
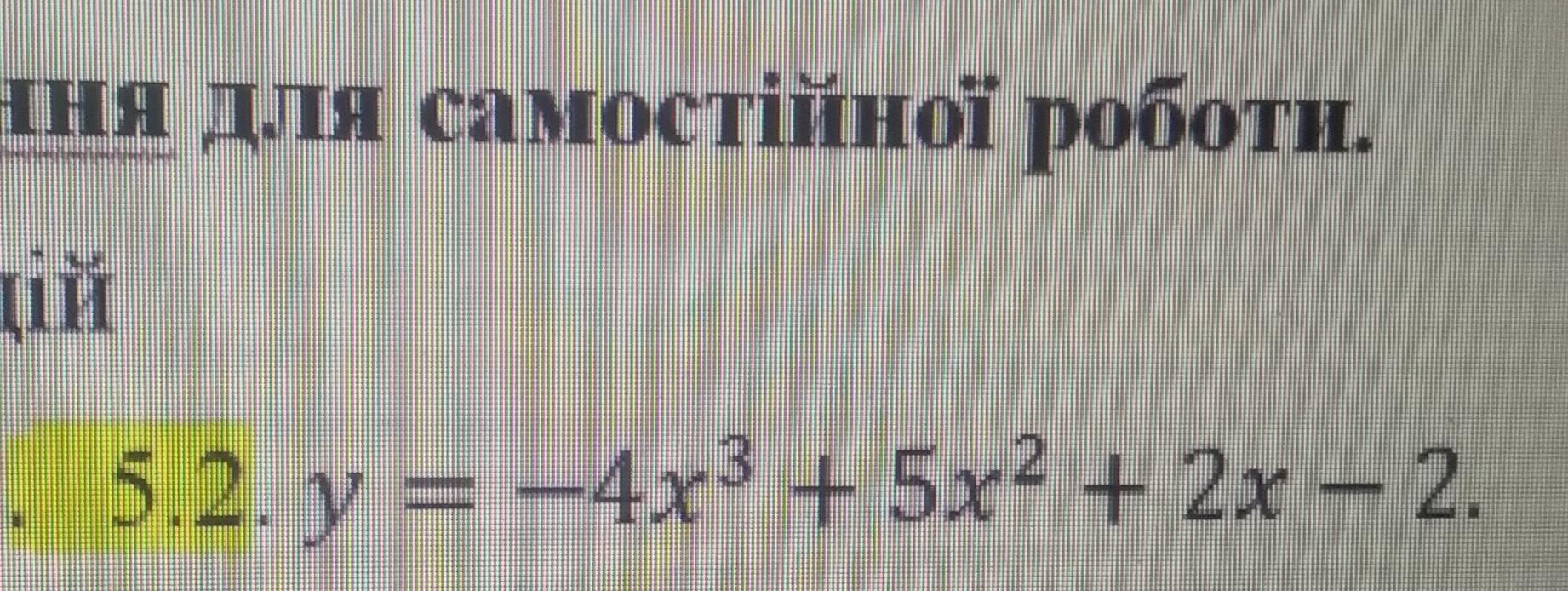
Ответы
Автор ответа:
0
Ответ:
Точка (1;1) - точка локального максимума функции y.
Точка - точка локального минимума функции y.
Примечание:
По таблице производных:
Пошаговое объяснение:
Так как , то при x = 1 функция имеет локальный максимум.
Так как , то при x =
функция имеет локальный минимум.
Точка (1;1) - точка локального максимума функции y.
Точка - точка локального минимума функции y.
Похожие вопросы
Предмет: Русский язык,
автор: aliyasat2009
Предмет: Математика,
автор: egormachacha62
Предмет: Другие предметы,
автор: aseevaalina334
Предмет: Русский язык,
автор: cka47