Question

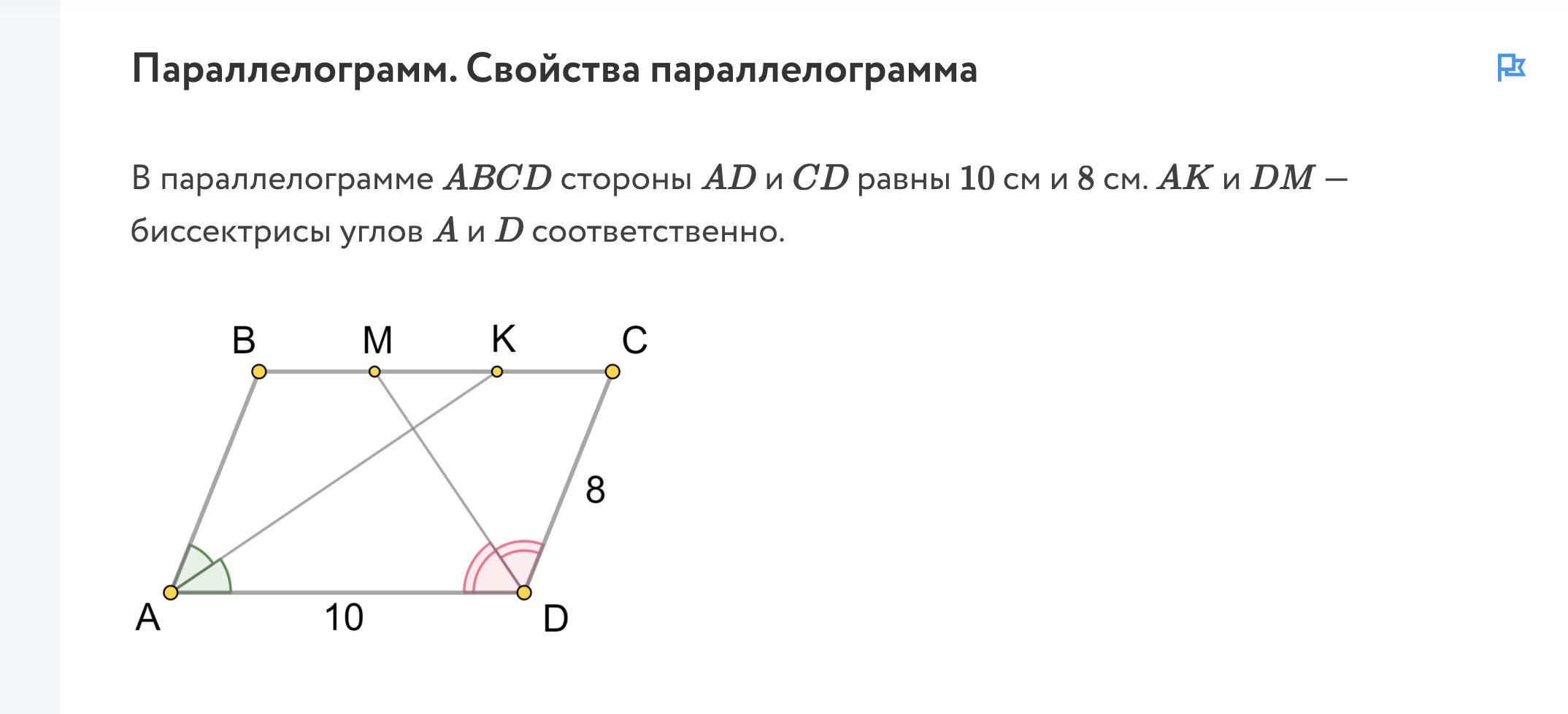
В параллелограмме ABCD стороны AD и CD равны 10 см и 8 см. АК и DM - биссектрисы углов А и D соответственно.

1. Найдите BM (в см).
2. Найдите МК (в см).
3. Укажите градусную меру угла между прямыми АК и MD.

Answer 1

Объяснение:

1)

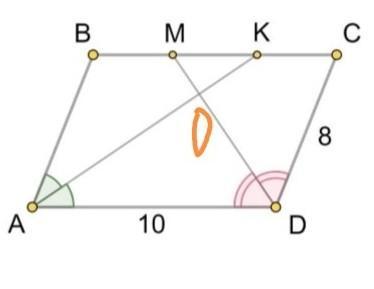
Биссектриса DM отсекает равнобедренный треугольник МСD,где МС=СD=8 см .

ВС=АD=10 см

ВМ=ВС-МС=10-8=2 см

2)

биссектриса АК отсекает равнобедренный треугольник АВК,где ВК=АВ=8 см,т.к

АВ=СD=8 см.

КС=ВС-ВК=10-8=2 см

МК=ВС-ВМ-КС=10-2-2=6 см

3)

найти : АОD

∠ОАD=x°

∠BAD=2∠ОАD=2x°,т.к АК - биссектриса

сумма углов прилежащих к одной стороне равна 180:

∠АDC=180-∠BAD=180-2x

∠ADO=∠ADC/2=(180-2x)/2=90-х ,т.к DM - биссектриса.

∠АОD=180-∠OAD-∠ADO=

=180-х-(90-х)=180-х-90+х=90°