Математика даю 100 балов за решеніе задачі на картінке частина(4)

Ответы
Ответ:
Площадь меньшего диагонального сечения равна см².
Пошаговое объяснение:
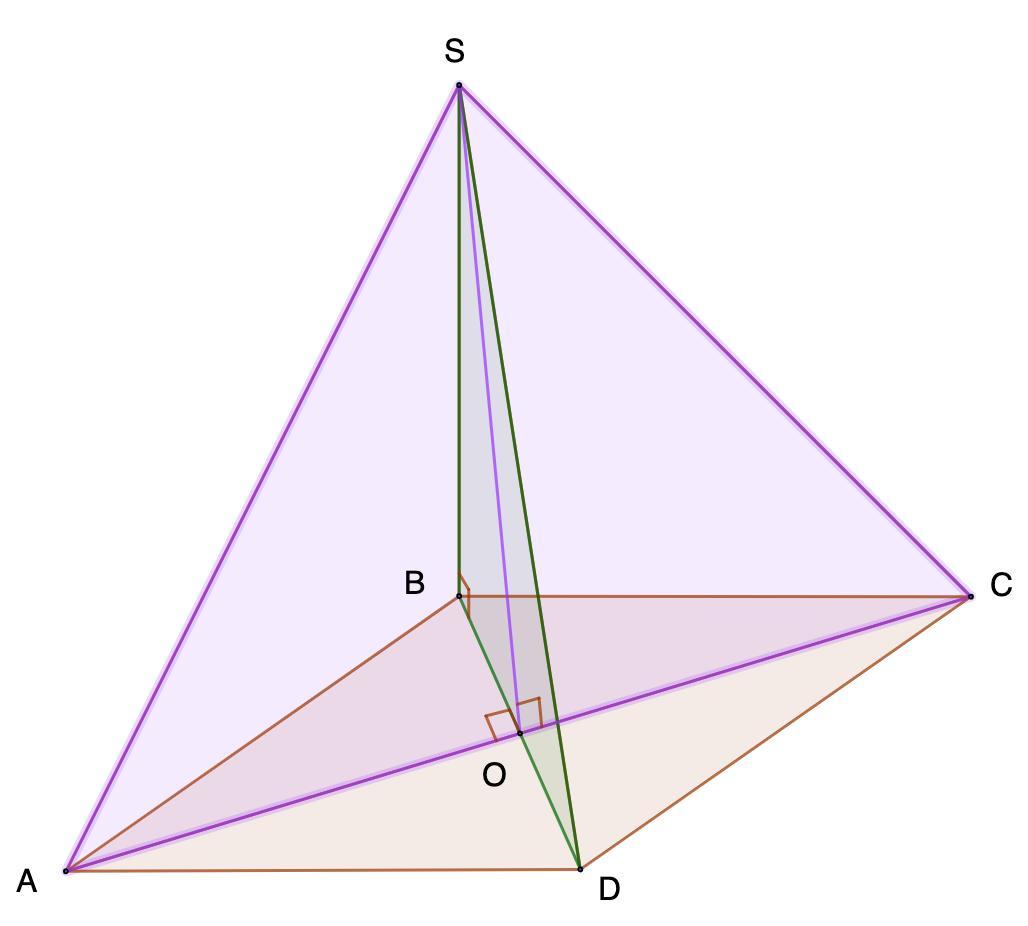
Основание пирамиды - квадрат с периметром 4а см. Две смежные боковые грани пирамиды перпендикулярны плоскости основания. Площадь большего диагонального сечения равна b. Найдите площадь меньшего диагонального сечения.
Дано: SABCD - пирамида;
АSB ⊥ ABCD; BSC ⊥ ABCD;
ABCD - квадрат;
P(ABCD) = 4a см;
Площадь большего диагонального сечения равна b см².
Найти: площадь меньшего диагонального сечения.
Решение:
- Диагональное сечение пирамиды — сечение пирамиды, проходящее через вершину и диагональ основания.
У нас два диагональных сечения: ΔACS и ΔBCD.
Определим, какое из них большее.
Рассмотрим ABCD - квадрат.
P(ABCD) = 4a см ⇒ сторона основания равна а.
- Диагонали квадрата равны, взаимно перпендикулярны и точкой пересечения делятся пополам.
⇒ АC = BD = a√2 (см)
Рассмотрим ΔBCD.
- Если две плоскости, перпендикулярные к третьей плоскости, пересекаются, то их линия пересечения есть перпендикуляр к этой плоскости.
⇒ SB ⊥ ABCD
- Если прямая перпендикулярна плоскости, то она перпендикулярна любой прямой этой плоскости.
⇒ SB ⊥ BD.
ΔBSD - прямоугольный.
⇒
Рассмотрим ΔASC.
BO ⊥ AC
- Прямая, проведённая в плоскости через основание наклонной, перпендикулярная к её проекции на эту плоскость, перпендикулярна и самой наклонной.
⇒ SO ⊥ AC
Так как SB < SO (перпендикуляр и наклонная), то большее сечение - ΔASC.
(см)
Найдем SB.
Рассмотрим ΔBSO - прямоугольный.
см.
SB² = SO² - BO²
(см)
Теперь можем найти площадь.
(см²)