Предмет: Алгебра,
автор: mymy140
Помогите решить пожалуйста. 100 очков. Задание на фото.
Приложения:
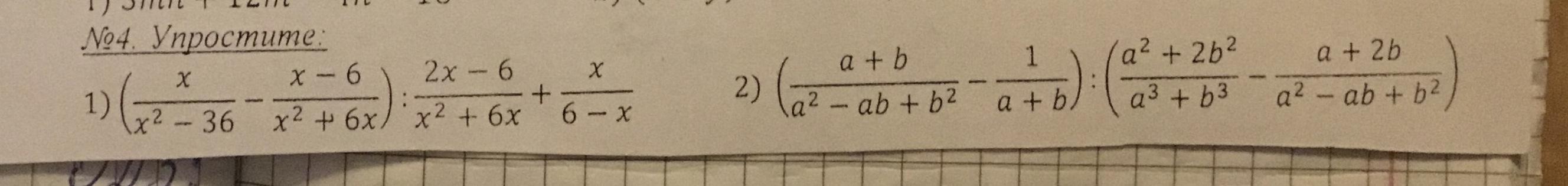
Ответы
Автор ответа:
1
Ответ:
Применяем формулы сокращённого умножения:
.
Похожие вопросы
Предмет: История,
автор: artompisarenko2
Предмет: Українська мова,
автор: artemiy83483882
Предмет: История,
автор: vikaakovenko4
Предмет: История,
автор: alimovayulduz11